- Schreiben Sie ein Struktogramm, das den Ablauf des Algorithmus beschreibt. Benutzen Sie hierzu den Struktogramm-Editor (Download).
- Notieren Sie eine Wertebelegungstabelle für die Behandlung der Zahl 90.
- Wählen Sie zur endgültigen Fehlerbereinigung weitere geeignete Testzahlen.
- Lesen Sie die untenstehende Meldung und untersuchen Sie, ob das angegebene n tatsächlich eine Primzahl ist.
- Implementieren Sie als V2 den Algorithmus rekursiv. Bedenken Sie welche Elementarbedingung zum Beenden der Rekursion führen muss.
- Erweiterungen: Zeigen Sie (optional) an, welcher Teiler gerade untersucht wird. Vergrößern Sie den Teiler geschickt (einmal um 1, dann immer um 2). Verwenden Sie hierzu nicht die (zeitkritische) IF...THEN...-Struktur.
Am 3. Dezember 2003 wurde gemeldet:
Ein Zusammenschluss tausender Computer
hat zur Entdeckung der bislang größten Primzahl geführt.
Das Konzept des so genannten Distributed Computing hat einen neuen
Erfolg zu vermelden. Wie das Great Internet Mersenne Prime Search-Projekt
(GIMPS) auf seinen Internetseiten mitteilt, konnte der Zusammenschluss
von 211.000 Rechnern die 40. Mersenne-Primzahl ermitteln. Bei einer
Mersenne-Primzahl handelt es sich um ein Zahlengebilde, das durch
die Konstruktion "2 hoch n minus 1" dargestellt werden
kann, wobei n ebenfalls eine Primzahl sein muss. Im aktuellen Fall
ist n gleich 20.996.011 - die Primzahl selbst hat 6,3 Millionen
Ziffern.
Die Ehre, die Primzahl entdeckt zu haben, gebührt
einem 26-jährigen Studenten aus dem US-Bundesstaat Michigan.
Sein mit 2-GHz getakteter Pentium-Rechner führte im weltweiten
Computerverbund die entscheidenden Berechnungen durch, die zur Ermittlung
der Mersenne-Primzahl führten.
Am 3. Januar 2006 wurde gemeldet:
Zwei amerikanische Professoren haben die bislang größte Primzahl entdeckt. Sie hat ausgeschrieben mehr als 9,15 Millionen Stellen (genau 9 152 052), wie das Internet-Primzahlenprojekt GIMPS (Great Internet Mersenne Prime Search) in Orlando (US-Staat Florida) berichtet.
Die jetzt größte Primzahl heißt mathematisch 2 hoch 30 402 457 minus 1. Cooper und Boone hatten sie mit Hilfe von 700 Computern entdeckt. Sie ist inzwischen von einem Forschungszentrum im französischen Grenoble bestätigt worden. Die Entdeckung hätte auf einem einzelnen durchschnittlichen PC rund 4500 Jahre benötigt, betont das Primzahlenprojekt GIMPS.
Die neue Primzahl ist erst die 43. entdeckte so genannte Mersenne-Primzahl. Der Name geht auf den französischen Mönch Marin Mersenne aus dem 17. Jahrhundert zurück. Mersenne-Primzahlen haben die Formel (2 hoch n) - 1.
Download für Schüler:
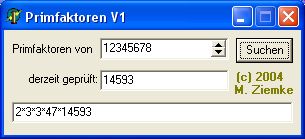
- Demoprogramm V1
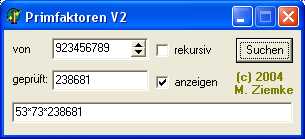
- Demoprogramm V2 (rekursiv)
Download nur für den Lehrer: