Original: Programmierungstechnik II
Quelle: https://wwwswt.informatik.uni-rostock.de/deutsch/Mitarbeiter/michael/lehre/pt2_sommer99.html
Dateien
![]()
![]() Arbeiten mit Dateien
Arbeiten mit Dateien
![]()
![]() Dateioperationen
Dateioperationen
Sortieren
![]()
![]() Grundsätzliches
Grundsätzliches
![]()
![]() Sortierproblem
Sortierproblem
![]()
![]() Inversionen
Inversionen
![]()
![]() Aufwandsabschätzung
Aufwandsabschätzung
![]()
![]()
![]()
![]() Beweise
Beweise
![]()
![]()
![]()
![]()
![]()
![]() O(f(n))
+ O(f(n))
O(f(n))
+ O(f(n)) ![]() =
= ![]() O(f(n))
O(f(n))
![]()
![]()
![]()
![]()
![]()
![]() c O(f(n))
c O(f(n))
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]() O(f(n))
O(f(n))
![]()
![]()
![]()
![]()
![]()
![]() O(f(n))
O(g(n))
O(f(n))
O(g(n)) ![]()
![]() =
= ![]() O(f(n)
g(n))
O(f(n)
g(n))
![]()
![]() Sortierverfahren allgemein
Sortierverfahren allgemein
![]()
![]()
![]()
![]() InsertSort
(Kochrezept)
InsertSort
(Kochrezept)
![]()
![]()
![]()
![]() InsertSort
(Verlauf)
InsertSort
(Verlauf)
![]()
![]()
![]()
![]() Insertsort mit Indizes (Kochrezept)
Insertsort mit Indizes (Kochrezept)
![]()
![]()
![]()
![]() Insertsort mit Indizes (Verlauf)
Insertsort mit Indizes (Verlauf)
![]()
![]()
![]()
![]() ShellSort
(Kochrezept)
ShellSort
(Kochrezept)
![]()
![]()
![]()
![]() ShellSort
mit Umspeichern der Elemente (Verlauf)
ShellSort
mit Umspeichern der Elemente (Verlauf)
![]()
![]()
![]()
![]() Countsort
(Kochrezept)
Countsort
(Kochrezept)
![]()
![]()
![]()
![]() Countsort
(Verlauf)
Countsort
(Verlauf)
![]()
![]()
![]()
![]() SelectSort
(Kochrezept)
SelectSort
(Kochrezept)
![]()
![]()
![]()
![]() SelectSort
(Verlauf)
SelectSort
(Verlauf)
![]()
![]()
![]()
![]() SelectSort mit Umspeichern der Elemente (Kochrezept)
SelectSort mit Umspeichern der Elemente (Kochrezept)
![]()
![]()
![]()
![]() SelectSort mit Umspeichern der Elemente (Verlauf)
SelectSort mit Umspeichern der Elemente (Verlauf)
![]()
![]()
![]()
![]() HeapSort
(Kochrezept)
HeapSort
(Kochrezept)
![]()
![]()
![]()
![]() HeapSort
(Verlauf)
HeapSort
(Verlauf)
![]()
![]()
![]()
![]() BubbleSort
(Kochrezept)
BubbleSort
(Kochrezept)
![]()
![]()
![]()
![]() BubbleSort
(Verlauf)
BubbleSort
(Verlauf)
![]()
![]()
![]()
![]() MergeSort
(Kochrezept)
MergeSort
(Kochrezept)
![]()
![]()
![]()
![]() MergeSort
(Verlauf)
MergeSort
(Verlauf)
![]()
![]()
![]()
![]() Quicksort
(Kochrezept)
Quicksort
(Kochrezept)
![]()
![]()
![]()
![]() Quicksort
(Verlauf)
Quicksort
(Verlauf)
![]()
![]()
![]()
![]() HybridSort
(Kochrezept)
HybridSort
(Kochrezept)
![]()
![]()
![]()
![]() HybridSort
(Verlauf)
HybridSort
(Verlauf)
Modulare Programmierungstechniken (Exkurs)
![]()
![]() Strukturierte Programmierung
Strukturierte Programmierung
![]()
![]() Module
Module
![]()
![]() Bibliotheken
- DLLs
Bibliotheken
- DLLs
![]()
![]() Objektorientierte Programmierung
Objektorientierte Programmierung
![]()
![]() Beispiel
Menge
Beispiel
Menge
Suchen Update zum "k-Problem"
![]()
![]() Median-Algorithmus
Median-Algorithmus
![]()
![]() Hashing
Hashing
![]()
![]()
![]()
![]() Hashing
mit Verkettung
Hashing
mit Verkettung
![]()
![]()
![]()
![]() Hashing mit offener Adressierung
Hashing mit offener Adressierung
![]()
![]() Suchen in geordneten Mengen
Suchen in geordneten Mengen
![]()
![]() Bäume
Bäume
![]()
![]()
![]()
![]() Allgemeines
Allgemeines
![]()
![]()
![]()
![]() Suchbäume
Suchbäume
![]()
![]()
![]()
![]() Blattsuchbäume
Blattsuchbäume
![]()
![]()
![]()
![]() Höhenbalancierte
Bäume
Höhenbalancierte
Bäume
![]()
![]()
![]()
![]()
![]()
![]() AVL-Bäume
AVL-Bäume
![]()
![]()
![]()
![]()
![]()
![]() (a, b)-Bäume
(a, b)-Bäume
![]()
![]()
![]()
![]()
![]()
![]() Rotation und
Doppelrotation
Rotation und
Doppelrotation
![]()
![]()
![]()
![]() Gewichtsbalancierte
Bäume
Gewichtsbalancierte
Bäume
![]()
![]()
![]()
![]() Gewichtete Bäume
Gewichtete Bäume
Verifikation
von Programmen
![]()
![]() Allgemeines
Allgemeines
![]()
![]() Technik
Technik
![]()
![]() Beispiele
Beispiele
![]()
![]()
![]()
![]() Verifikation von Anweisungen zum Vertauschen zweier
Variablen
Verifikation von Anweisungen zum Vertauschen zweier
Variablen
![]()
![]()
![]()
![]() Verifikation einer Multiplikation durch Aufsummierung
Verifikation einer Multiplikation durch Aufsummierung
![]()
![]()
![]()
![]() Verifikation einer linearen Suche
Verifikation einer linearen Suche
![]()
![]()
![]()
![]() Verifikation von Code zur Ermittlung des ggT
Verifikation von Code zur Ermittlung des ggT
![]()
![]()
![]()
![]() Verifikation
von Code zur Berechnung der Fakultät einer Zahl
Verifikation
von Code zur Berechnung der Fakultät einer Zahl
![]()
![]() Einschränkungen
Einschränkungen
Die im folgenden verwendete Variable Datei kann die Verbindung zu
sein.
Typisierte Dateien
Typisierte Dateien enthalten Datensätze konstanter Länge.
Zwischen den Datensätzen ist kein Trennzeichen vorhanden.
Deklaration: var Datei : File of MeinDatentyp;
| 1 | ABC | x | 99991111 | o |
| 2 | BCD | - | 00002222 | o |
| 3 | CDE | x | 12345678 | o |
Sinnvoll ausgelesen werden kann eine solche Datei nur mit einer entsprechenden Datenstruktur, etwa:
record
zähler : integer;
kuerzel : string[3];
marker : char;
kundennr : string[8]
status : char;end;
Zum Lesen und Schreiben muß keine Unterscheidung beim Zugriff getroffen werden, das datensatz-orientierte Hin- und Herspringen ermöglicht jegliche Zugriffe auf eine Datei, wenn sie geöffnet ist.
Binärdatei/untypisierte Datei
Hierbei handelt es sich genauer besehen um eine Spezialform
der typisierten Datei mit Datensätzen der Länge 1 Byte.
Deklaration: var Datei : File;
bzw ... var Datei : File of Byte;
Der Aufbau ist allgemein somit eine Reihe von Byte:
| 68 | 72 | 67 | 255 | 24 | 177 | 14 | 13 | 163 | 192 | 201 | 82 | 66 | 104 | 19 | 99 |
Textdateien
Deklaration: var Datei : textfile;
Testdateien sind zeichen- und zeilenweise organisiert, Zeilen
werden durch die Sonderzeichen Wagenrücklauf (13) und
Zeilenvorschub (10) abgeschlossen:
| Eine Textzeile, ziemlich lang. | 13 | 10 |
| eine weitere ... | 13 | 10 |
| und noch eine ... | 13 | 10 |
Dateioperationen (Auswahl)
Assign(Datei, 'c:\temp\daten.dat')
Ordnet der Variablen Datei die durch die Zeichenkette 'c:\temp\daten.dat' angegebene Datei zu, eine Pascal-interne Variable wird mit einem Bezeichner auf Betriebssystem-Ebene verbunden.
Assign ist in Delphi ersetzt durch AssignFile.
Reset(Datei)
Rewrite(Datei)
Read(Datei, EinDatensatz)
Write(Datei, EinDatensatz)
Seek(Datei, Satznummer)
Seek setzt den Datensatzzeiger auf den seiner Nummer entsprechenden Datensatz.
Close(Datei)
Close schließt eine geöffnete Datei.
Close ist in Delphi ersetzt durch CloseFile.
sonst.: NIL-Zeiger können auf Dateien durch Datensätze mit der Satznummer -1 abgebildet werden.
Weitere Informationen:
Online-Hilfe der Inprise-/Borland-Entwicklungsumgebungen
Doberenz, Walter und Kowalski, T., Borland Delphi 2 für Profis. Carl Hanser Verlag, München, 1996
(Jaa, richtig, das ist kein Turbo-Pascal sondern ein Delphi-Buch - in dem Buch zum Pascal-Nachfolger läßt sich jedoch auch zu den vorigen Versionen brauchbares Wissen in ziemlich gut lesbarer Form finden.)
Sortieren erfordert bestimmte Voraussetzungen. Die Folge
S = {a, A, ASCII(65), A, 1000001}
enthält zwar Elemente, die alle eindeutig und voneinander unterscheidbar sind, sich aber auf den ersten Blick nicht vernünftig sortieren lassen. Dies ginge erst, wenn weitere Kriterien gefunden wären, nach denen sortiert werden soll - etwa die Schönheit eines Ausdrucks, die benötigten Kurven, der Aufwand für die Repräsentation etc.
Neben der Unterscheidbarkeit der Elemente wird also auch ein Kriterium benötigt, daß die Elemente sich ihrer dann ergebenden Größe nach 'ordenbar' macht. Die Mathematik drückt das etwa so aus:
x, y Î M ® x > yÚ x<yÚ x = y
Das heist: Ordnen von Elementen einer Größe nach funktioniert über paarweises Vergleichen. Hierbei kann bei einem Paar Elemente entweder das eine oder das andere Element größer sein oder es sind beide gleich .
x, y, z Î M ® x < y Ù y < z ® x < z
Wenn ein Element kleiner als ein anderes ist, bleibt es gegenüber einem noch größeren Element (natürlich) das kleinere.
Treffen diese Eigenschaften auf Elemente einer Menge zu, bezeichnet man sie als geordnete Menge. Auf geordneten Mengen lassen sich Sortierungen sinnvoll durchführen.
Ein Sortierproblem liegt vor, wenn eine Folge von Elementen einer geordneten Menge gegeben ist, und eine bestimmte Permutation (d. h. eine Anordnung der Elemente einer Menge) der Elemente gewünscht ist, beispielsweise 'aufsteigend der Größe nach', oder ähnlich.
Eine Inversion zwischen Elementen einer Folge liegt vor, wenn zwei Elemente innerhalb dieser Folge der gewünschten Ordnung entgegen einsortiert sind. In der Folge
S = {2, 1, 3, 4, 5, 6, 7, 8, 9}
liegt genau eine Inversion zwischen den Elementen a1 und a2 vor.
Ein Maß zur Einschätzung des Zustands einer Folge bezüglich
seiner Sortiertheit ist die Anzahl der Inversionen.
Die Folge
S = {1, 2, 3, 4}
weist keine Inversion auf, der Grad der Sortiertheit ist somit
0, die Folge ist 'sortiert'.
Bei der Folge
S = {3, 1, 4, 2}
hingegen kann a1 gegen a2 und a4 invertiert werden sowie a3 gegen a4, somit liegen 3 Invertierungen vor, der Grad der Sortiertheit ist also 3.
Da der Aufwand für die Arbeit mit Elementen in aller Regel mit der Anzahl der Elemente steigt, sucht man Funktionen, die den Aufwand eines Algorithmus in Abhängigkeit genau dieser Anzahl beschreibt.
In der Regel interessiert man sich für drei Größen:
In allen Fällen interessiert in der Regel die Größenordnung des errechneten Aufwands. Ergibt beispielsweise die exakte Analyse eines Algorithmus den Rechenzeitaufwand
T(n) = 4 n3 + 2 n2 + 25
heißt das für die Größenordnung des Aufwands einfach
O(n) = n3
Es interessiert für eine Aufwandsabschätzung also lediglich der Term mit der höchsten Ordnung ohne Faktoren und ohne Summanden. Darüber hinaus bleiben auch Terme erhalten, die die betrachtete Größe n als Variable beinhalten wie z.B. n × log n oder n × sqrt(n) (auch bei solchen Termen wiederum keine Faktoren oder Summanden).
g(n) = O(f(n))
bedeutet, im schlimmsten Fall liegt der Aufwand für g(n) £ c × f(n). Die genaue Definition des O-Kalküls:
O(f(n) = {g: N ® N | $ n0 > 0, $ c > 0 :" n ³ n0 : g(n) £ c × f(n)}
Hieraus können Rechenregeln abgeleitet werden wie beispielsweise
O(f(n)) + O(f(n))
=
O(f(n))
c O(f(n))=
O(f(n))
O(f(n)) O(g(n))=
O(f(n) g(n))
die sich auch beweisen lassen.
Beweise zur Aufwandsabschätzung
Beweisidee: Finden der Darstellung, die für die linke Seite die Konstanten c2 und c2 liefert, die sich zu einer Konstante c zusammenfassen lassen, damit sichtbar wird, dass bei der Addition von Aufwänden keine höhere Aufwandsklasse entsteht, als die der Summanden.
Der linke Summand O(f(n)) läßt sich durch g1(n) substituieren, da per Definition mit
g1(n) = O(f(n)) auch g1(n) £ c1 × f(n) gilt.
Es entsteht
g1(n) + O(f(n)) = O(f(n))
Ebenso kann mit dem zweiten Summanden verfahren werden. Mit
g2(n) = O(f(n)) gilt auch hier g2(n) £ c2 × f(n)
Also kann man auch folgendes schreiben:
g1(n) + g2(n) = O(f(n))
g1(n) und g2(n) lassen sich zu g(n) zusammenfassen:
g1(n) + g2(n) = g(n)
Setzt man für g1(n), g2(n) und g(n) die Abschätzungen ein, kommt man auf
c1 × f(n) + c2 × f(n) = (c1 + c2) × f(n)
Mit der Substitutiun von c1 + c2 = c kann man
g(n) £ c × f(n)
setzen. Dies entspricht
g(n) = O(f(n))
und beweist die These.
O(f(n)) heißt, der Aufwand eines Verfahrens g läßt sich nach oben durch die Funktion c f(n) abschätzen (also: g ist - ab einer bestimmten Anzahl n von Elementen - immer kleiner als eine sorgsam gewählte Funktion f - versehen mit dem Faktor c1), also
g(n) £ c1 f(n) (das entspricht der Definition)
Wird nun das Verfahren um den Faktor c aufwendiger (und das ist der Fall der nun eigentlich bewiesen werden soll), ergibt sich durch beidseitiges Einfügen des Faktors
c g(n) £ c c1 f(n)
Die rechte Seite dieser Gleichung enthält zwei Konstanten, die durch eine Substitution c2 = c c1 auf die Gleichung
c g(n) £ c2 f(n)
führt.
Dies entspricht auf der rechten Seite wieder der Definition und zeigt somit, daß ein weitere konstanter Faktor c die Größenordnung des Aufwands nicht beeinflußt.
O(f(n)) O(g(n)) = O(f(n) g(n))
Die Behauptung bedeutet zunächst: Der Gesamtaufwand eines Verfahrens v setzt sich zusammen aus f(n) Durchläufen eines Verfahrens v1 und aus g(n) Durchläufen eines Verfahrens v2.
Hierauf läßt sich zweimal in gleicher Weise aufbauen:
- O(f(n)) bedeutet, der Aufwand des Verfahrens v1 läßt sich nach oben durch die Funktion c1 f(n) abschätzen.
- O(g(n)) bedeutet, der Aufwand des Verfahrens v2 läßt sich nach oben durch die Funktion c2 g(n) abschätzen.
Für den Gesamtaufwand des Verfahrens v = v1 v2 folgt hieraus die Zusammensetzung der beiden Abschätzungen c1 f(n) c2 g(n).
Hierbei können die Faktoren c1 und c2 zu c zusammengefaßt werden
c = c1 c2
und erhalten dann den Aufwand c f(n) g(n) dessen Größenordnung O wiederum O(f(n) g(n)) ist.
...
SIGNATUR
![]()
![]() sort:
sort: ![]()
![]()
![]()
![]()
![]()
![]() Tab
Tab ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -> Tab
-> Tab
![]()
![]() insert_sort: Tab x Key x Elem ->
Tab
insert_sort: Tab x Key x Elem ->
Tab
...
AXIOMS
![]()
![]() sort(init)
sort(init)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() = init
= init
![]()
![]() sort(errtab)
sort(errtab)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() = errtab
= errtab
![]()
![]() sort(c(t, k, e))
sort(c(t, k, e))![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]() insert_sort(sort(t),
k, e)
insert_sort(sort(t),
k, e)
![]()
![]() insert_sort(init,
k, e)
insert_sort(init,
k, e)![]()
![]()
![]()
![]()
![]()
![]()
![]() = c(init, k, e)
= c(init, k, e)
![]()
![]() insert_sort(c(t,
k, e), k1, e1) = if e1 < e
insert_sort(c(t,
k, e), k1, e1) = if e1 < e
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() then
c(insert_sort(t, k1, e1), k, e)
then
c(insert_sort(t, k1, e1), k, e)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() else c(c(t, k ,
e), k1, e1)
else c(c(t, k ,
e), k1, e1)
Bisher haben sich trotz vieler verschiedener Sortier-Algorithmen nur vier wirklich grundlegend verschiedene Vorgehensweisen zum Sortieren herauskristallisiert:
Die Voraussetzung um überhaupt sinnvoll sortieren zu können ist, daß ein Sortierproblem vorliegt: Vereinfacht:
($ (Folge mit Elem. für die die Relation 'kleiner als' def. ist))
Sortieren läßt sich also auf verschiedene Art und Weise - aber ist das alles dasselbe? Das wäre nicht schlecht - man bräuchte dann nur noch eines zu beherrschen. Tatsächlich ist dem anders, daher gibt es verschiedene Kenngrößen für Sortieralgorithmen.
Unter der Stabilität versteht man die Eigenschaft, Vorsortierungen nicht zu verändern. Dies ist relevant, wenn die zu sortierenden Elemente mehrfach vorkommen können und deren Auftreten in dieser Folge zueinander bereits die gewünschte Reihenfolge darstellt. Speicheraufwand bedeutet, was man sich auch darunter vorstellt - wieviel Speicher wird für Variablen, Abbildungen der Folge, etc. benötigt, ebenso der Rechenaufwand - wieviele Operationen müssen in Abhängigkeit der zu bearbeitenden Elemente durchgeführt werden. Natürlich ist allgemein ein Algorithmus besser, der 10.000 Elemente mit 20.000 Operationen sortieren kann, als einer, der 400.000.000 Schritte dazu braucht. Allgemein - benötigt jener erste möglicherweise aber für die 10.000 Elemente zweimal soviel Speicher wie der wesentlich langsamere und ist Zeit vorhanden, Speicher jedoch absolut nicht, kann ein in einer bestimmten Hinsicht schlechterer Algorithmus wieder sehr attraktiv werden.
Kurzum: Einige Sortierverfahren und einige Kenngrößen hierzu sollten bekannt sein, mit nur einem Verfahren und seiner Arbeitsweise kann es in der Praxis etwas eng werden.
Für alle Beispiele wird die Folge {49, 67, 331, 96, 21, 332, 58, 74} benutzt.
Idee (einfachster Ansatz):
Insertsort mit Indizes (Kochrezept)
InsertSort mit Indizes/Listenverarbeitung (Verlauf)
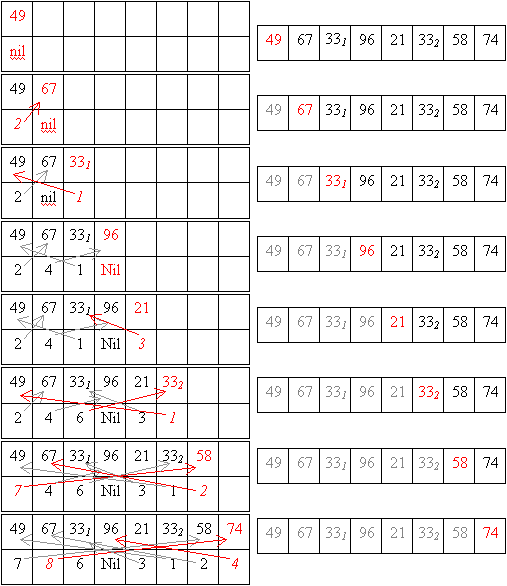
ShellSort mit Umspeichern der Elemente (Verlauf)
Phase 1 (mit n = 5, also 5 Elemente Abstand beim Umsortieren):
Phase 2 (mit n = 3, somit 3 Elemente Abstand beim Umsortieren):
Phase 3 (mit n = 1, also Umsortieren benachbarter Elemente):
(weiter mit InsertSort oder BubbleSort)
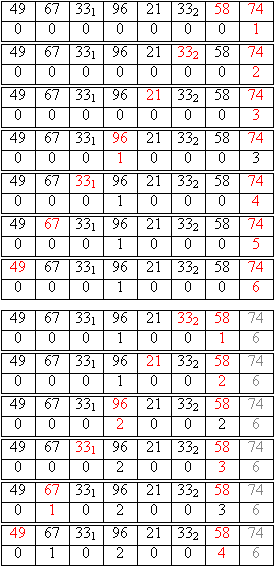
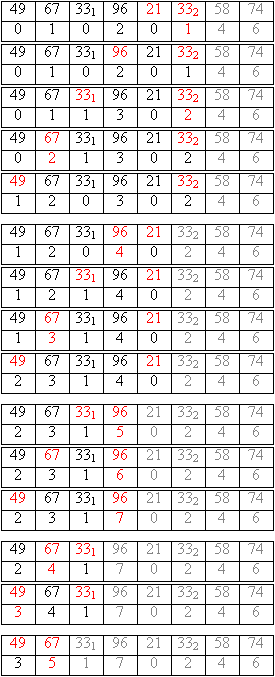
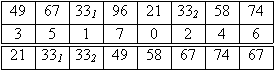
Übertragen der Zahlen in Reihenfolge der Werte der Hilfsfolge:
SelectSort mit Umspeichern der Elemente (Kochrezept)
SelectSort2 mit Umspeichern der Elemente (Verlauf)
Heapsort ist ein Algorithmus, der am besten über die Struktur von bestimmten Bäumen (sog. Heaps) gut verstehbar ist. Prinzipiell wird Heapsort zur Sortierung von Folgen angewandt, wobei die Folgen baumartig behandelt werden.
Ein Heap ist ein Baum mit folgenden Eigenschaften:
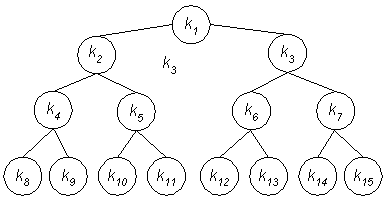
Kurzum besteht Heapsort aus zwei Phasen: einmal werden heapartige Bäume aufgebaut und zum anderen werden die inneren Heapeigenschaften hergestellt.
Schritt 1: Aufbau des Heaps
Unsere Folge
![]()
wird zunächst in eine Baumstruktur umgetopft, d.h. der Reihe (von links nach rechts und von oben nach unten) nach über die Blätter verteilt. Bei einer Folge mit acht Elementen ergeben sich somit vier Heapebenen:

Als Baum notiert:
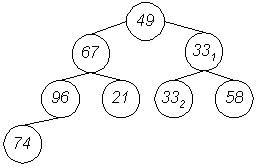
Hierin befinden sich 4 mögliche Heaps (die Stellung der Elemente ist noch zufällig und bedarf mit hoher Wahrscheinlichkeit Korrekturen):
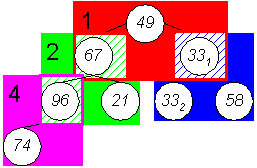
Schritt 2: Herstellung der Heapeigenschaft
Die Herstellung der Heapeigenschaft geschieht von unten nach oben und von rechts nach links durch Vertauschen von Elementen. Verglichen werden drei Werte je Heap. Das Maximum der drei Werte muß an die Stelle des Vaterknotens gebracht - entweder der größte Wert befindet sich bereits zufällig an dieser Stelle oder es wird der entsprechende Wert eines Sohnknotens mit dem bisherigen Vaterknoten ausgetauscht.
1. Durchlauf
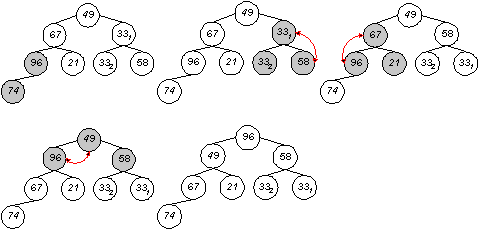
Der maximale Wert befindet sich nun in der Wurzel des Baumes, es ist gefunden und kann - nachdem es in irgendeiner Form 'gemerkt' wurde - entfernt werden. Das entstandene Leck an der Wurzel wird mit dem letzten Element des Heaps aufgefüllt:
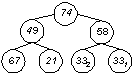
Ergebnis:
![]()
2. Durchlauf:

Ergebnis:
3. Durchlauf:
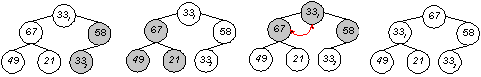
Ergebnis:
4. Durchlauf:

Ergebnis:
5. Durchlauf:

Ergebnis:
6. Durchlauf:
![]()
Ergebnis:
7. Durchlauf:
![]()
Ergebnis:
![]()
Die Folge und das Flag zum Vermerken der Veränderung innerhalb eines Durchlaufs:
![]()
1. Durchlauf:
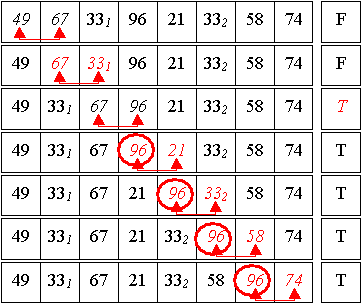
Gut zu sehen ist hier das blasenartige Aufsteigen des größten Elements der Folge, daher der Name Bubblesort. Es gab mindestens eine Umsortierung (das Flag wurde auf True gesetzt), daher erfolgt - nach dem Zurücksetzen des Flags - ein weiterer Durchlauf.
2. Durchlauf:
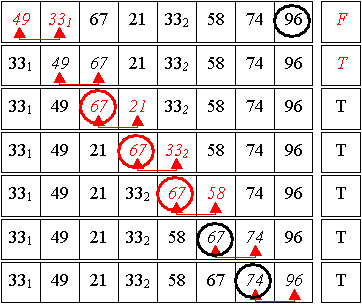
Es gab mindestens eine Umsortierung => Flag zurücksetzen + ein weiterer Durchlauf ...
3. Durchlauf:
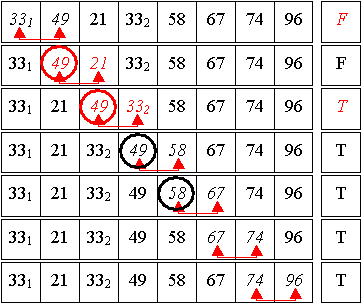
Es gab mindestens eine Umsortierung => Flag zurücksetzen + ein weiterer Durchlauf ...
4. Durchlauf
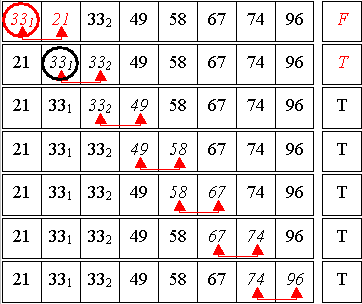
Es gab mindestens eine Umsortierung => ein weiterer Durchlauf ...
5. Durchlauf

Bei diesem Durchlauf fand keine Umsortierung mehr statt (das Flag ist am Ende des Durchlaufs immer noch auf False gesetzt), Bubblesort ist beendet und die Folge sortiert.
Ähnlich wie in Heapsort wird also auch hier in zwei Schritten verfahren
- eine bestimmte Struktur erzeugt
- aus dieser Struktur heraus sortiert
Erzeugen von Teilfolgen durch jeweils mittiges Teilen von Folgen, und verbinden der minimalen Folgen zu sortierten Folgen nächstgrößerer Ordnung durch Einfügen des kleinsten Elements von links (da die nächstgrößere Ordnung zwei-elementige Folgen darstellen, sind zwei Schritte notwendig, im ersten Schritt wird das größere Element in die Verbindungsfolge übertrage, im zweiten Schritt werden die übrigen Elemente übertragen).

Aus den zwei-elementigen Teilfolgen werden nun sortierte vier-elementige Teilfolgen aufgebaut.
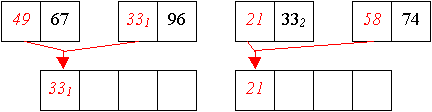
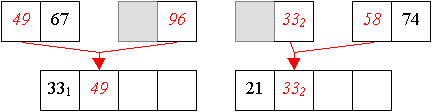
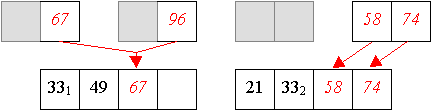
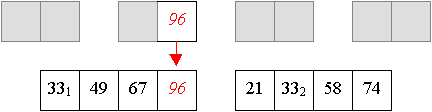
Und aus zwei vier-elemtigen Folge wird nun eine sortierte acht-elemtige Folge erzeugt:
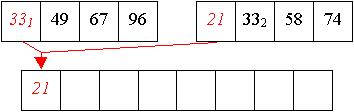
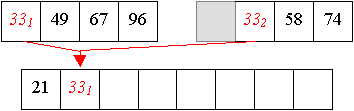
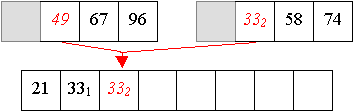
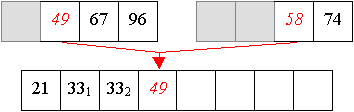
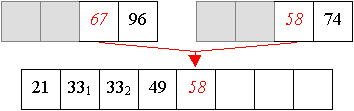
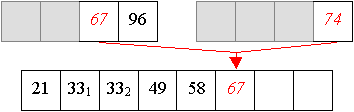
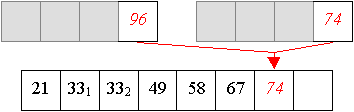
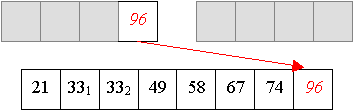
Auch Quicksort arbeitet in zwei Phasen,
1. Teilen der Folge
Aus der zu sortierenden Folge
![]()
wird ein beliebiges Element (Pivotelement), z.B. das erste Element gewählt:
![]()
Die Folge wird nun in zwei Teilfolgen geteilt, wobei die linke Teilfolge alle Elemente kleiner dem Pivotelement enthalten soll und die rechte Teilfolge alle Elemente größer dem Pivotelement.
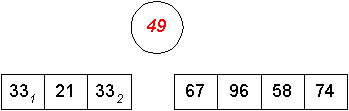
Dieser Schritt wird bezogen auf die entstehenden Teilfolgen fortlaufend wiederholt:
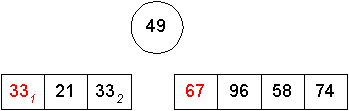
Verteilen der Elemente der Folgen in Teilfolgen mit der Eigenschaft, daß die Elemente links vom Pivotelement kleiner oder gleich diesem Element sind und die Teilfolgen rechts des Pivotelements die größeren Elemente umfassen:
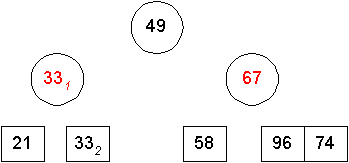
Erneutes Anwenden, Pivotelement wählen:
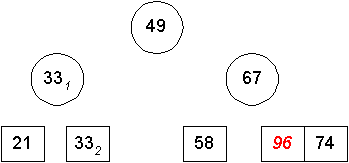
Teilfolge erzeugen (hierbei tritt der Fall einer leeren Teilfolge auf):
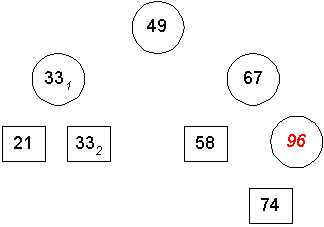
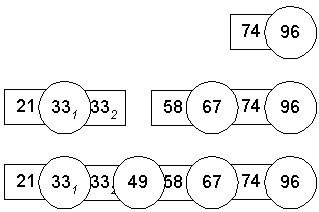
2. Zusammensetzen durch Verbinden der untersten noch vorhanden Teilfolgen mit dem Pivotelement in der Mitte als Verbindungsglied:
Das Zusammensetzen erfolgt hierbei in drei Schritten.


Modulare Programmierungstechniken
Das allgemeine Vorgehen strukturierter Programmierung läßt sich wie folgt beschreiben: Ein Problem wird zerlegt in Teilprobleme und in Beziehungen zwischen diesen Teilproblemen. Neben dieser allgemeinen Beschreibung wird auch die Programmierung anhand von Konstrukten verstanden, die sich mit Diagrammen nach Nassi-Shneiderman erfassen lassen - diese Seite soll aber in diesem kontext nicht weiter interessieren.
Hilfreich für die Zerlegung in Teilprobleme ist, wenn diese Zerlegung auch durch eine sinnvolle Aufteilung im Quelltext wiedergegeben werden können und nicht ein seitenlanger Quelltext vorliegen muß. Ein erster Ansatzpunkt hierfür sind Funktionen und Prozeduren, die letzenendes eine Form von Unterprogrammen darstellen. Erreichen läßt sich hiermit zumindest eine Art thematische Katalogisierung von Routinen. Syntaktisch hat so etwas folgende Gestalt:
unit routines;
interface
procedure do_a(x : integer);
procedure do_b(y : integer);
implementation
procedure do_a(x : integer);
begin
x := x;
end;
procedure do_a(y : integer);
begin
y := y;
end;
end.
Anstelle des sonst üblichen Schlüsselwortes zum Programmbegin program steht nun das Wort unit, neu ist auch das Wort interface, hierunter werden die Teile der Unit aufgeführt, die von außen benutzbar sein sollen, vergleichbar einer public signature in den ADTs. Intern ist es also möglich weitere Routinen zu erzeugen, die von außen nicht aufrufbar sein sollen, dies wird als Information Hiding bezeichnet.
Ein Hinweis hierzu: Man sollte sich hierbei und bei den folgenden Beispielen bewußt machen, daß es sich bei diesen Prinzipien, um Lösungen für Probleme handelt, die auftreten, wenn mit hunderten oder gar tausenden von Elementen gearbeitet werden muß, also mit einer Menge Code, in der selbst einfaches Scrollen zum minutenlangen Akt werden kann. Die in solchen Beispielen wie hier übliche handvoll Routinen könnte man natürlich zunächst fast immer ohne jene Zusatztechnologien beherrschen.
Unter einem Modul versteht die Informatik eine in sich geschlossene Programmeinheit bestehend aud Konstanten, Variablen, Datentypen und Operationen. Eine reinen Routinensammlung wie wird nun also ergänzt um einen eigenen inneren Zustand (siehe unterstrichene Zeilen):
unit encapsulated;
interface
procedure do_a(x : integer);
procedure do_b(y : integer);
implementation
var i : integer;
procedure do_a(x : integer; var i : integer);
begin
i := x^2;
end;procedure do_b(y, i : integer);
begin
y := i + y;
end;end.
Modular aufgebaut ist ein System, wenn es aus abgrenzbaren Einheiten zusammengesetzt ist und wenn diese Einheiten einzeln ausgetauscht, verändert oder hinzugefügt werden können, ohne daß andere Teile des Systems beeinflusst werden (Bsp. HiFi-Anlage: Ein neues Tapedeck sollte sich nicht auf die Klangeigenschaften des CD-Players auswirken).
Für uns ergibt sich ab hier eine neue Handlungsweise: Während sich im Rahmen eines einfachen Prozedurkonzepts nur Operationen zerlegen lassen, ist durch das Modulkonzept auch eine Aufteilung der Daten (Datentypen, Variablen, Konstanten) möglich.
Wie Module eingebunden werden, hängt von der jeweiligen Programmiersprache und ggf. auch von deren Implementierung ab.
Merkmale modulorientierter Programmierung
Aspekte der Strukturierung können berücksichtigt werden:
Die Wiederverwendbarkeit von Code kann unterstützt werden:
Aspekt des Schutzes
Bei Datenkapseln handelt es sich um nach außen abgeschirmte Verbunde aus Daten und Algorithmen. Anders ausgedrückt: Das Innere der Datenkapsel (die Implementation) bleibt nach außen verborgen.
Eine Datenkapsel (z. B. eine entsprechend genutzte Unit) kann nur über die im Interfaceteil definierten Felder und Methoden angesprochen werden. Das Innere der Unit (der Implementationsteil) bleibt nach außen verborgen. Mechanismen zur Modularisierung sind für die Bildung von Datenkapseln notwendige Voraussetzungen. Das Konzept der Datenkapsel entspricht hier dem ersten Anschein nach zunächst dem von Modulen, aus heutiger Sicht haben Datenkapseln aber hierüber weit hinaus geführt, hin zur objekt-orientierten Programmierung und zu komponenten-orientierten Programmiersystemen.
Im folgenden zwei Beispiele hierfür. Es sei vereinbart, für ein System die Funktionen Init, Store und Show zur Verfügung zu stellen, Init richtet hierbei Speicher für kommende Eingaben aus, Store fügt die übergebenen Elemente in den Speicher ein und Show zeigt die eingegebenen Elemente an. Eine denkbare Implementierung hierfür könnte folgendes Stück Code darstellen:
unit Kapsel;
interface{ was sichtbar sein soll ... }
procedure Init;
procedure Store(elem : string);
procedure Show;implementation
var { unsichtbar }
a : array[1..20] of string;
i : 0..20;
procedure Init;
begin
i := 0;
end;procedure Store(elem : string);
begin
if i < 20
then begin
i := i + 1;
a[i] := elem;
end;
end;procedure Show;
var k : integer;
begin
for k := 1 to n do writeln(a[k]);
readln;
end;end.
Nun eine von der ersten Umsetzung abweichende Implementierung, dennoch muß in einem System, daß auf die Unit Kapsel lediglich über die per Interface zur Verfügung stehenden Schnittstellen zugreift, nichts geändert werden. Die Implementierungsdetails spielen praktisch keine weitere Rolle.
unit Kapsel;
interfaceprocedure Init;
procedure Store(elem : string);
procedure Show;implementation
var f : text;
procedure Init;
begin
assign(f,'Daten.tmp');
rewrite(f);
close(f);
end;procedure Store(elem : string);
begin
append(f);
writeln(f, elem);
close(f);
end;procedure Show;
var zeile : string;
begin
reset(f);
while not eof(f) do
begin
readln(f,line);
writeln(line);
end;
close(f);
end;end.
Obwohl sich nahezu die gesamte Implementierung von Beispiel 1 zu Beispiel 2 verändert hat, bleiben die folgenden Funktionsaufrufe unverändert gültig:
program kap;
uses kapsel;
begin
init;
store(‚a‘);
show;
end.
DLLs sind compilierte Modulbibliotheken, die in andere Programme eingebunden werden können. Achtung: Der Begriff Bibliothek hat an dieser Stelle nichts mit Klassen-Bibliotheken im objekt-orientierten Sinne (VCL, OWL, MFC, JFC etc.) zu tun, hierzu kommen wir weiter unten.
Vorteile:
Vorsicht: Groß- und Kleinschreibung wird hierbei - anders als in Pascal sonst - unterschieden! Der für die Erzeugung einer DLL notwendige Rahmen, wird von Delphi weitgehend generiert, nur seine Routinen muß man selber erzeugen und in die exports-Klausel aufnehmen (dies entspricht der interface-Anweisung in normalen Units, die dort eher einen Header als einen Anhang darstellt).
library Project1;
uses SysUtils, Classes;procedure a(n : integer);
begin
{ ... }
end;function b(n : integer) : integer;
begin
{ ... }
end;exports
procedure a; stdcall;
function b; stdcall;
begin
end.
Der Aufruf entsprechender Routinen gestaltet sich in Pascal wie folgt:
procedure a; stdcall; external ‘demo.dll‘;
function b; stdcall; external ‘demo.dll‘;
Objektorientierte Programmierung
Überblick
Die strukturierte Programmierung erwies sich in der Vergangenheit als ungenügend, wenn die Projekte eine bestimmte Größe annahmen oder Systeme mit hoher Komplexität vorlagen. Gesucht wurde daher ein Konzept nach folgenden Kriterien:
Die entwickelte Unterstützung zur Implementierung großer Projekte die OOP, verzichtet zur Erfüllung dieser Kriterien auf die optimale Ausnutzung der individuellen Leistungsmerkmale der jeweiligen Maschine.
Die Realisierung - Objekte
Grundlage der OOP ist eine neue Datenstruktur, die als Klasse bezeichnet wird. Von diesen Klassen können Instanzen geildet werden, sogenannte Objekte, diese sind Informationsträger mit zeitlich veränderbarem Zustand, für die definiert ist, wie sie sich bei bestimmten Nachrichten bzw. Botschaften (eingehende Mitteilungen an ein Objekt) zu verhalten haben [Engesser93]. Objekte sind heterogene Datenstrukturen, ähnlich records in Pascal oder structs in C. Im Gegensatz zu den genannten Datenstrukturen werden bei Objekten die datenbezogenen Objektfelder und die damit zusammenhängenden Prinzipien zur Verarbeitung enger aneinandergebunden (sowie ferner liegende Zugriffe nicht mehr zugelassen). Funktionen und Prozeduren (allgemein mit dem Oberbegriff Routinen bezeichnet, im OOP-Bereich Methoden genannt), die der Manipulation von Daten dienen, werden nun mit den betreffenden Daten zusammen ‘aufbewahrt’, dieses Vorgehen wird als Kapselung bezeichnet. Datenstrukturen (im folgenden als Daten bezeichnet) und Running-Code (im folgenden als Code bezeichnet) sind nicht mehr beliebig über das ganze Programm verteilt.
Diese anfangs banal erscheinende Ordnung hat sich in der Praxis bezüglich der oben aufgestellten Forderungen als mächtiges Gestaltungsmerkmal erwiesen. Elementar ist, daß jedes Objekt die ausschließliche Kompetenz und Verantwortung für die Verarbeitung seiner Objektdaten hat. Zugriffe auf die Daten eines Objekts einer Klasse sind nur mit den objekteigenen Methoden zulässig.
Das ursprüngliche Konzept für den Umgang mit Daten und Code
Eine Simulation der Population von Vogelarten könnte herkömmlich wie folgt aussehen: Verschiedene Vögel werden berücksichtigt, darunter Papagei, Albatrosse, Kanarienvögel und Raben
program vogel;
type papagei = record
gewicht : real;
groesse : real;
alter : integer;
farbe : integer;
sprache : boolean;
end;
kanarienvogel = record
gewicht : real;
groesse : real;
alter : integer;
farbe : integer;
gesang : boolean;
end;
albatross

=
record
gewicht : real;
groesse : real;
alter : integer;
farbe : integer;
landung : boolean;
end;
mortalrate = real;
natalrate = real;
geschwind = real;begin
end.
Nach den Daten wird der ausführbare Code modelliert und im folgenden eine Auswahl hierzu möglicher Routinen:
programm a;
procedure bestand(var anzahl : integer; zeit : integer;
mortalrate, natalrate : real);
begin
...
endprocedure strecke(ort : integer; geschwind : real);
begin
...
end;function JaegerVerlust(rate : real; anzahl : integer) : real;
begin
...
end;function FangVerlust(rate : real; anzahl : integer) : real;
begin
...
end;begin
end.
Ein Merkmal dieser Art der Datenverarbeitung ist ein hoher Grad an programmiertechnischer Freiheit:
Die Integration von Code und Daten
Eine objektorientierte Herangehensweise würde aus den Vogelarten eine Klasse TVogel modellieren - eine sogenannte Basisklasse, die diejenigen benötigten Felder enthielte, die möglichst viele Vogelarten teilen
programm a;
type TVogel = class
gewicht : real;
groesse : real;
alter : integer;
farbe : integer;
procedure bestand(anzahl, zeit : integer;
mortalrate, natalrate : real);
procedure strecke(ort : integer; geschwind : real);
function JaegerVerlust(rate: real; anzahl: integer);
end;
begin
end.
Diese Datenstruktur stellt nun die Grundlage für die weitere Entwicklung dar und muß in dieser Form nur einmal geschrieben werden, man bezeichnet dies daher als Basisklasse bzw. abstrakte Basisklasse, aufgrund ihrer Eigenschaft als Obermenge häufig auch als Superklasse; abstrakt nennt man diese Klassen deswegen, weil TVogel nur zum Bilden der eigentlichen Vogelarten benutzt wird, Variablen dieser Klasse (Instanzen genannt) jedoch nie erzeugt werden. Zusätzlich kann die Möglichkeit der Erzeugung von Instanzen aus abstrakten Klassen in vielen Sprachen unterbunden werden.
Bis hier sieht es nicht danach aus, als könnte man Code sparen, der fundamentale Schritt steht jedoch noch bevor - die Vererbung. Der Weg, um aus der Klasse TVogel zum Beispiel den Papagei zu entwickeln, geht nicht über das Abschreiben oder Einfügen per Maus sondern über Vererbung - man deklariert eine neue Klasse und leitet es aus der Basisklasse mit dem Schlüsselwort class ab:
type TPapagei = class(TVogel)
end;
Die Klasse TPapagei besitzt durch diese Deklaration aufgrund des wirkenden Vererbungsprinzips alle Datenfelder und Codeanteile der vererbenden Klasse, Elternklasse genannt.
Dies für sich ist jedoch nicht ausreichend um erheblich effizienter zu programmieren - TPapagei soll schließlich ein Erbe von TVogel sein und keine Kopie, genau das ist aber bisher der Fall. Das Prinzip der Vererbung sieht daher auch Manipulationen vor. So läßt sich TPapagei erweitern, indem man Datenfelder und ausführbaren Code in Form von Funktionen und Prozeduren hinzufügt (im folgenden als Methoden bzw. als Memberfunktionen bezeichnet).
Da Papageien als Haustiere interessant sind, könnte auf deren Population neben natürlichen Feinden auch noch eine überproportional hohe Fangquote einwirken, ein Datum, daß man genau im Falle der Papageien berücksichtigen möchte; in diesem Falle könnte eine Vererbung mit Erweiterung wie folgt aussehen:
programm a;
type TPapagei = class(TVogel)
rate : real;
function gefangen(rate : real; anzahl : integer) : real;
end;
begin
end.
Die Deklaration in diesem Listing führt demnach zu einer Klasse TPinguin, die die Felder und Methoden von TVogel geerbt hat und in der Implementierung (die hier nicht modelliert wird) der Methode bestand von der ursprünglich geerbten Methode aller Wahrscheinlichkeit nach abweicht (sonst wäre es redundant, sie erneut zu schreiben), also einer Klasse, die der in folgendem Listing entspricht - ohne den gesamten Code explizit schreiben zu müssen
type TPinguin = class(TVogel)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() gewicht:
real;
gewicht:
real;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() groesse:
real;
groesse:
real;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() alter
: integer;
alter
: integer;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() farbe
: integer;
farbe
: integer;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() procedure
bestand(anzahl, zeit : integer; mortalrate,
natalrate : real);
procedure
bestand(anzahl, zeit : integer; mortalrate,
natalrate : real);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() procedure
strecke(ort : integer; geschwind :
real);
procedure
strecke(ort : integer; geschwind :
real);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() function
JaegerVerlust(rate : real; anzahl :
integer);
function
JaegerVerlust(rate : real; anzahl :
integer);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() end;
end;
Die enorme Effizienz der objektorientierten Programmierung erwächst aus der Tatsache, daß eine Basisklasse oder allgemein auch Elternklasse (jede vererbende Klasse), deren Korrektheit getestet ist, vererbt werden kann, ohne bei den Nachfahren dieselbe Arbeit wiederholen zu müssen. Das Kriterium der Wiederverwendbarkeit des Codes ist hiermit erfüllt; wie der wenige zu schreibende Code dennoch zu viel Kodierung führt, sollte prinzipiell deutlich geworden sein - wenn auch die Effizienz eines Prinzips für tausende Zeilen Code hier an einigen dutzend Zeilen nur schemenhaft skizziert werden kann.
Die Kapselung von Daten und Code stellt das Organisationsprinzip objektorientierter Programmierung dar; allerdings wäre die Kapselung alleine eine relativ passive Unterstützung, da die Verantwortung damit verbliebe, wo sie vorher war, beim Programmierer. Vor allem in großen Projekten mit mehreren Programmierern bietet die herkömmliche strukturierte Programmierung in imperativen Sprachen viele Fehlerquellen aufgrund der mächtigen Freiheiten:
Gekapselte Datenstrukturen könnten ebenso beliebig manipuliert werden. Die Zuweisung von Werten an ein Feld eines Verbundes (siehe Listing 10)
type papagei = record
alter : integer;
...
end;
var p1 : papagei;
begin
...
p1.alter := 2;
{direkte Zuweisung an Record-Komponente}
...
end.
würde zu einer Art ‘Klassen-Verbund-Zuweisung’:
type TPapagei = class(TVogel)
alter : integer;
...
end;
var p1 : TPapagei;
begin
...
p1.alter := 2;
{stilistisch schlecht: direkte Zuweisung
an eine Komponente eines Objekts}
...
end.
Hiermit würde die Komponente alter des Objekts p1 der Klasse TPapagei identisch zur Variablen alter des Verbundes TPapagei benutzt und die Schutzmechanismen der objektorientierten Vorgehensweise prinzipiell aufgehoben. Dies würde nur vermieden, wenn ein Programmierer die Disziplin hätte, solche direkten Zuweisungen an Objektfelder nicht zu schreiben. Programmierumgebungen, die objektorientiertes Programmieren unterstützen, setzen bereits beim Entwurf an, indem
Diese Zugriffskontrolle wird allgemein als Information Hiding bezeichnet. Der Begriff ist in diesem Kontext nicht ganz korrekt, da es hier weniger um das Verbergen von Information geht. In aller Regel trifft eher zu, daß Zugriffe unterbunden werden.
Das hier vorliegende Beispiel zeigt, wie man Vererbung und Kapselung einsetzen kann um Mengen im mathematischen Sinne zu Modellieren. Anstelle einiger Funktionen und Variablen spielt es nun eine größere Rolle als früher, wo etwas steht. Unser bisheriges Herangehen hat hier, sofern es der Syntax des Compilers nicht widersprach, nicht viele Limitierungen gekannt - nun gilt es hier vielfältige Designentscheidungen zu treffen.
Der Code selbst veranschaulicht den Einsatz der Strukturen in Delphi, ist syntaktisch korrekt, aber nicht lauffähig und daher nicht weiter getestet (Lehrbeispiel einer Todsünde, jawoll).
Generell gilt das Suchen als eine der wichtigsten und grundlegensten Operationen, die mit Rechnern ausgeführt werden, zum Beispiel die Stichwortsuche in Enzyklopädien und Suchmaschinen oder auch die Suche nach Telefonnummern in entsprechenden Verzeichnissen.
Erster Ansatz hierzu ist ein Universum U aus Schlüsseln, anhand derer die tatsächliche Information ermittelt werden kann. Formal:
U = { 0, ..., k-1 }n, n ist die Länge des Strings über dem Alphabet
Weitere Begriffe hierzu:
- Schlüsselmenge S: eine Teilmenge aus einem Universum U
- Schlüssel: Element aus der Schlüsselmenge zur Kennzeichnung einer Information
- Information: zu speichernde Daten, die mit einem assoziierten Schlüssel Wiedergefunden werden können
- Statisches Suchen: das Suchen verändert die vorhandenen Datenstrukturen nicht
- Dynamisches Suchen: die Schlüsselmenge wird zur Optimierung des Suchvorgangs umstrukturiert (z. B. Suchmaschinen im Web ändern ihre Datenstrukturen um in Abhängigkeit von Rankings auf andere Resultate zu kommen)
- Median: Elementk mit k = n/2 aus einer Menge mit n Elementen (also: der Schlüssel, dessen Index in der Mitte der Schlüsselmenge angesiedelt ist). In der unsortieren Menge {5, 7, 1} stellt 5 den Median dar.
Erster Ansatz für Suchalgorithmen: Suche nach dem kleinsten Schlüssel in einer Schlüsselmenge. Ist dieser ermittelt, läßt er sich aus der Schlüsselmenge nehmen und aus der Restmenge erneut der kleinste Schlüssel finden. Dieser Ansatz wäre gleichbedeutend mit dem Ansatz, anstelle des kleinsten Schlüssels den größten zu suchen. Beides ist mit diesem Vorgehen von erträglichem Aufwand, solange wirklich nur in den Randbereichen der Schlüsselmengen gesucht wird. Läuft dies jedoch in den mittleren Bereich einer Menge oder prinzipiell zum Median - womit im schlimmsten Fall natürlich gerechnet werden muß, fällt der generell hohe Aufwand deutlich und negativ auf. Einen leistungsfähigeren Ansatz stellt der Median-Algorithmus zur Ermittlung des i-kleinsten Schlüssels dar.
Gegeben sei eine Schlüsselmenge S = {9, 4, 1, 8, 3, 6, 5} und der Median-Algorithmus, der dem Suchbefehl finde(i, S) zugrundeliegt. Der Ablauf des Algorithmus in Form eines Struktogramms:
Was liefert nun also der Aufruf finde(5, S)?
Erster Durchlauf:
1: Ein Pivotelement - der Einfachheit halber das erste: e := 9
(die 9 wird nun nicht mehr berücksichtigt, außer es kommt zur Ausgaberoutine)
2: S1 := {m | m Î S, m < e}, d. h. S1 = {4, 1, 8, 3, 6, 5}
3: S2 := {m | m Î S, m > e}, d. h. S2 = {}
4: | S1| = 6, d. h. | S1| > i – 1 => finde(5, S1)
Zweiter Durchlauf:
5: e := 4
6: S1 := {1, 3}
7: S2 := {8, 6, 5}
8: | S1| = 2, d. h. | S1| < i – 1 => finde(i - |S1| - 1, S2), also i = 2 und finde(2, S2)
Dritter Durchlauf:
9: e := 8
10: S1 := {6, 5}
11: S2 := {}
12: | S1| = 2, d. h. | S1| > i – 1 (da i – 1 = 1) => finde(2, S1)
Vierter Durchlauf:
13: e := 6
14: S1 := {5}
15: S2 := {}
16: | S1| = 1, d. h. | S1| = i – 1 => ausgabe(e) = 6
Tatsächlich ist das Element 6 das fünft-kleinste Element. Die Sortierung von {9, 4, 1, 8, 3, 6, 5} führt auf {1, 3, 4, 5, 6, 8, 9}.
Ansatz: Zum Finden eines Schlüssels k wird (anstelle von Vergleichen mit anderen Schlüsseln) eine Berechnung durchgeführt, die auf den Schlüssel k zu einem Datensatz führen soll. Das heißt, das Finden eines Elements hängt möglichst nur noch von der Komplexität der Berechnung ab (kann also nahezu konstant sein) und muß nicht mehr grenzenlos mit der Anzahl der Elemente steigen (allenfalls noch mit der Stelligkeit).
Die Datensätze werden in einem linearen Feld mit Indizes [0, ..., m – 1] gespeichert, der Hashtabelle (in der Literatur auch Hashtafel, das ist nix anderes), m ist die Größe der Hashtabelle. Das heißt, es liegt ein Feld folgender Art vor:
type HashTable = array[0..m1] of tElement;
Die hierin aufgenommenen Datensätze können beispielsweise folgende Aufbau haben:
type tElement = record
Key: tKey;
Info: tInfo;
end;
Eine Abbildung, die Hashfunktion h : k ® {0, ... , m – 1} ordnet jedem Schlüssel k einen Index h(k) mit 0 £ h(k) £ m – 1 zu, die Hashadresse, k entstammt einer Untermenge S eines Universums U
U = {x | 0 £ x £ N - 1}, |U| = N, S Í U
Kriterien für Hashfunktionen:
Ein Beispiel für eine Hashfunktion ist etwa h(k) = k mod m.
Anwendung: Die Menge S = {57, 52, 68, 41, 72}soll in einem Feld
T: array [0..5] of integer ;
untergebracht werden.
Wir wählen beispielsweise h(k) = k mod 6
(natürlich hätte man hier auch etwas wirklich Abgefahrenes
wählen können), es ergibt sich für das Array(untere Zeile).
![]()
So weit, so gut. Die Menge und die Funktion waren optimal zueinander gewählt, Kollisionen traten nicht auf, realistisch muß aber auch folgender Fall erwogen werden, also etwa ...
Anwendung: S = {57, 52, 68, 41, 72, 12, 44, 63, 66}
Es sei wieder h(k) = k mod m, mit m
= 6, dann ergibt sich folgende Zuordnung:
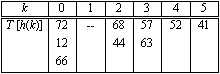
Es gibt mehrere Ergebnisse für h(k), beispielsweise führt die Suche nach dem Index 72 auf dasselbe Ergebnis, wie die Suche nach dem Index 12. Das heißt, für die unterschiedlichen Indizes k1 und k2 ergeben sich h(k1) und h(k2) mit der Eigenschaft h(k1) = h(k2), die Information hinter den genannten Indizes wäre zunächst nicht eindeutig wiederherstellbar, die Zuordnung ist nicht eindeutig.
Es bieten sich gelegentlich Hashfunktionen an, die keine Kollisionen erzeugen, sie werden bezeichnet als perfekte Hashfunktion. Läßt sich jedoch keine solche finden, gibt es zwei Strategien:
- Eine Verkettung der kollidierenden Elemente mit Durchlaufen der Kette im Suchfall.
- Offene Adressierung
Bei diesem Ansatz ist die Hashtabelle ein Feld von Listen, die i-te Liste enthält alle Elemente k mit h(k) = i. Neben der Berechnung der Hashfunktion ergibt sich hierbei die Notwendigkeit die möglichweise anhängigen Listen zu bearbeiten. Im Speicher ergibt sich ausgehend vom letzten Beispiel folgende Struktur:
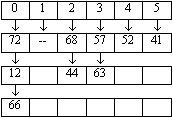
Realisierung verschiedener Operationen:
Suchen(k): Beginne bei [T[h(k)]] und Folge den Verweisen der Liste bis k gefunden oder nil erreicht ist
Einfügen(k): Wenn Suchen(k) erfolglos ist, wird das Element k am Ende der Überlaufkette eingesetzt oder in das berechnete Feld T[h(k)] eingefügt.
Entfernen(k): Wenn Suchen(k) erfolgreich verläuft, streiche das Element aus der Überlaufkette oder lösche es aus dem Feld T[h(k)] und setzte gegebenenfalls das erste Element der Überlaufkette dort ein.
Hashing mit offener Adressierung
Hierbei ist die Adresse eines Elements nicht eindeutig durch die Hashfunktion bestimmt, sondern es existiert zu jedem x Î U eine Folge von Adressen h(x, i) mit i = 0, 1, 2 ...
Ansatz ist hierbei die Unterbringung der Elemente nicht außerhalb der Hashtabelle in Form von Listen, sondern innerhalb der Hashtabelle. Ist der errechnete Platz für ein Element besetzt, muß nun ein anderes offenes Feld ermittelt werden.
Beispiel:
h(x, i) = (h1(x) + i × h2(x)) mod m
h1(x) = x mod 8
h2(x) = 1 + x mod 5
S = {22, 35, 41, 17, 19, 20}
h(22, i) = (22 mod 8 + i × (1 + 22 mod 5)) mod 8
= (6 + i × 3) mod 8
= 6
Dies gilt für i = 0, im Kollisionsfall könnte man nun i erhöhen, bis ein Platz gefunden ist, an dem keinerlei Kollisionen mehr auftreten. Dieses Vorgehen ist jedoch nicht unproblematisch, ein Schlüssel kann nun unauffindbar werden, wenn etwa Elemente gelöscht und andere Elemente dafür eingefügt worden sind, maßgeblich ist nämlich auch der Zeitpunkt des Einfügens. Infolgedessen ist das Löschen von Elementen ohne weitere Maßnahmen eine unzulässige Operation.
Für ein weiteres Problem benötigt man das Maß des Belegungsfaktors: Für eine Hashtabelle der Größe m, die n Schlüssel speichert, läßt sich der Quotient b mit b = n / m bilden, der sogenannte Belegungsfaktor. Ist der Belegungsfaktor b = 1, können ebenso Probleme bei der offenen Adressierung auftreten - wenn die Hashtabelle also voll ist, muß geregelt werden, was mit noch einzufügenden Elementen passiert.
Es kann in diesem Zusammenhang hilfreich sein, Funktionen als Parameter übergeben zu können. Ein Beispiel für den formalen Aufbau eines Delphi/Pascal-Programms befindet sich hier.
Eine geordnete Menge S = {x1, x2, ... , xn}, mit x1 < x2 < xn ist in Form eines geordneten Vektors gespeichert.
Der grundlegende Algorithmus zum Auffinden eines Elements in einer solchen Menge ist das "der Bibliothek des Kongresses".
Das Ganze in Form eines Struktogramms, eine Funktion IsIn(a, S) zum Finden eines Elements a in einer Menge S, deren Elemente ganze Zahlen aus N sein sollen:

Die erste Zeile schlägt vor, ein Element aus der Menge der Elemente zu nehmen, jedoch nicht welches. Tatsächlich ist egal, mit welchem Element begonnen wird, solange man alle Elemente die nötig sind, erreicht. Da aber zunächst kein Vorteil daraus entsteht, an einer sonderbaren Stelle anzufangen, bietet es sich hier (und im folgenden) an, einfach mit dem ersten Element der Menge zu beginnen.
Beispiel:
IsIn(15, S) mit der geordneten Menge S =
{2, 4, 12, 15, 19, 20}
Die Funktion wird in folgendem Ablauf abgearbeitet:
Wesentlich effizienter als diese lineare Suche ist die sogenannte binäre Suche. Der Aufwand läßt sich hiermit von O(n) auf O(log (n)) senken. Dies kann erreicht werden, indem lediglich die vorletzte Zeile im Struktogramm zu
Nächstes := (Untergrenze + Obergrenze)/2
geändert wird.
Suchalgorithmen für sich können nicht endlos optimiert werden, jedoch kann man mit dem Ansatz der binären Suche dafür sorgen, daß zu durchsuchende Mengen wie etwa Mengen von Schlüsseln zum Zugriff auf Informationen in such-optimierter Form abgespeichert sind. Algorithmus und geeignete Datenstruktur hängen hierbei also eng zusammen. Der Weg zum effizienten Suchen geht über Baumstrukturen, infolgedessen dreht sich dieser Abschnitt um die verschiedenen hier geeigneten Baumkonstrukte und um deren Erhalt/Wiederherstellung bei den verschiedenen Operationen.
Die Datenstruktur Baum und ihre Anwendungen sind im ersten Teil der Veranstaltung detailiert behandelt worden, im folgenden ein kurzes Resumée dessen, was wir im weiteren benötigen.
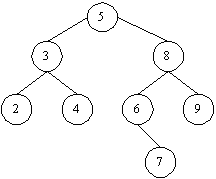
Ein Suchbaum (sieht nun also gar nicht so ungewöhnlich aus ...):
Suchen
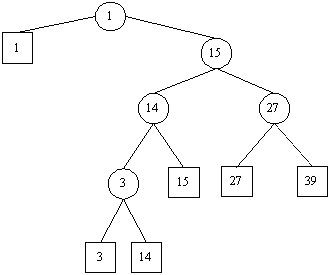
Eine Suchoperation Suche(p, x) in einem Suchbaum mit der Wurzel p nach dem Element x läuft wie folgt ab:
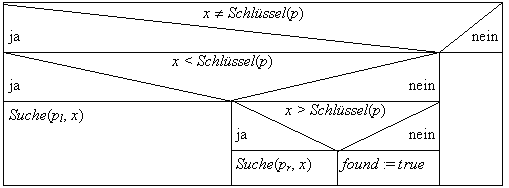
Einfügen
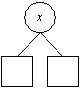
Um einen Schlüssel einzufügen, muß zunächst sichergestellt werden, ob er schon enthalten ist – er muß also gesucht werden. Die Suche endet innerhalb eines Suchbaumes nicht an einer beliebigen Stelle sondern an einer dem Pfad zufolge logischen Stelle, positiv (Schlüssel ist schon im Baum) oder negativ (der Schlüssel ist noch nicht Element des Baumes). Im negativen Falle wird der gewünschte Schlüssel einfach an der aktuelle Position eingefügt, das heißt das aktuelle Blatt, an dem es nicht weitergeht, wird durch einen Knoten ersetzt, dessen Wert der gewünschte Schlüssel ist, und an diesen werden zwei Blätter (Söhne) gehängt. Letzteres macht den Knoten zum inneren Knoten (¹ Blatt)
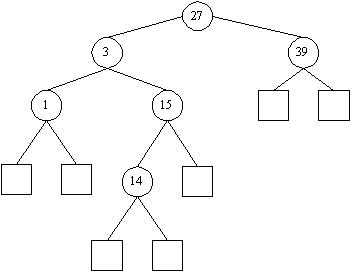
Der Beispielbaum bekommt beim Einfügen des Wertes 20 also folgende Gestalt:
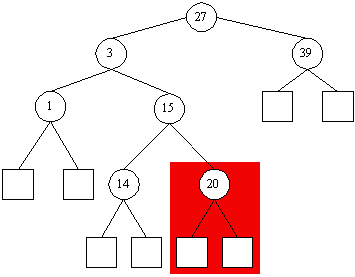
Der entstehende Baum für eine Menge von Elementen ist nicht eindeutig, je nachdem, wann welche Werte eingefügt werden, ergeben sich unterschiedliche Bäume. So wäre beispielsweise für die enthaltenen Elemente auch der folgende Baum korrekt:
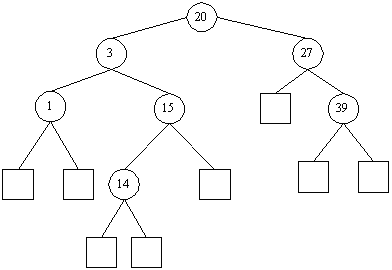
Dies für sich wäre kein Problem, allerdings kann es aufgrund der Zufälligkeit der Einfügeoperation auch vorkommen, daß ein Baum entartet bzw. degeneriert (beides in der Literatur üblich und meint: sich der Gestalt einer Liste annähert), im einfachsten Fall, wenn die Elemente zufällig alle der Größe nach eingefügt werden, so daß die vorgeschaltete Suchoperation immer auf dem rechten unteren Teilbaum endet (und infolgedessen eben genau dort einfügt):

Die Operationen die beschleunigt werden sollen, hätten nun aufgrund der linearen Gestalt linearen und keinen logarithmischen Aufwand mehr, gerade die optimierende Eigenschaft wäre aufgehoben. Hierzu später mehr (® höhenbalancierte Bäume).
Entfernen
Wichtig ist, daß man den Baum so hinterläßt, daß er wiederum einen gültigen Suchbaum darstellt. Auch das Entfernen beginnt wieder mit einer Suche, der zu löschende Schlüssel muß vorhanden sein und gefunden werden. Der symmetrische Nachfolger q von p (wird im Struktogramm benötigt) ist Knoten q mit dem kleinsten Schlüssel nach p und
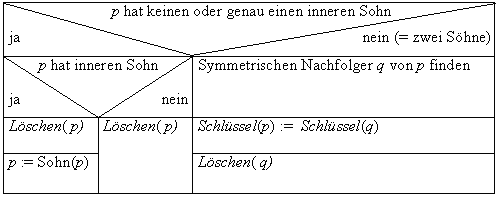
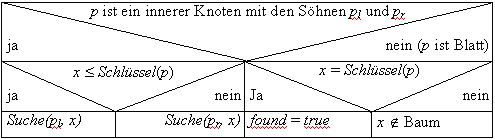
Suche(p, x) in einem Blattsuchbaum gestaltet sich wie folgt:
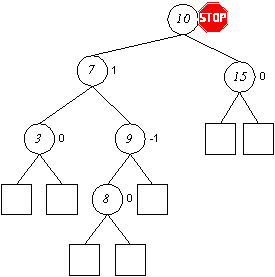
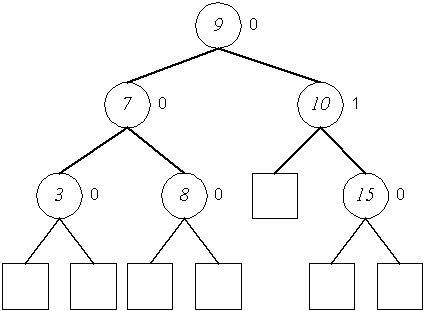
Bereits erwähnt wurde, daß Bäume strukturell zu Listen degenerieren können. Adelson-Velskij und Landis haben weitere Forderungen an den Aufbau von Bäumen geknüpft, Bäume die diesen zusätzlichen Regeln folgen, heißen nach ihren Entdeckern AVL-Bäume.
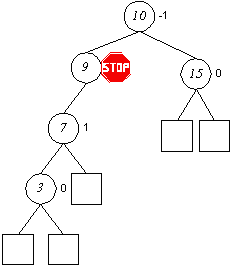
Beispiele:
Der linke und der rechte Baum erfüllen das zusätzlich eingeführte Kriterium für AVL-Bäume, für den mittleren läßt sich hingegen ein Knoten finden, dessen linker und rechter Teilbaum eine Differenz der Höhe um mehr als 1 aufweisen, er ist somit kein AVL-Baum.
Hieraus folgt unter anderem, daß die Beliebigkeit der Gestalt eines AVL-Baumes stark eingeschränkt ist, Listen ohne sinnvolle Verzweigungen sind unterbunden, die Höhe für eine Menge von n Elementen ist begrenzt auf log n.
Infolgedessen müssen die manipulierenden Operationen wie Einfügen und Löschen anders implementiert werden bzw. die neuen Forderungen mit umsetzen, das Suchen hingegen bleibt unverändert, da AVL-Bäume weiterhin auch binäre Suchbäume sind und der Suchvorgang sich somit also nicht unterscheidet.
Einfügen in AVL-Bäumen (Rotation, Doppelrotation)

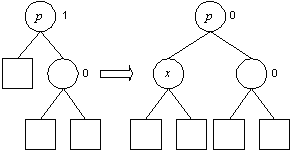
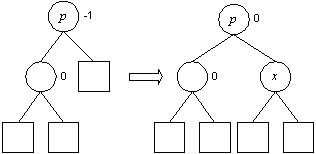
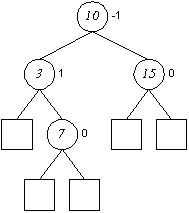
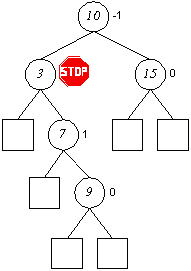
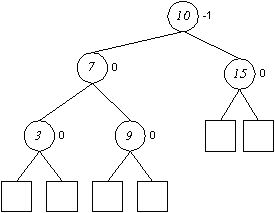
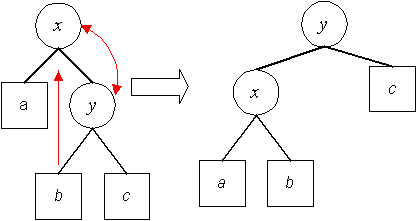
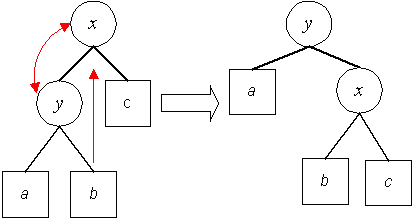
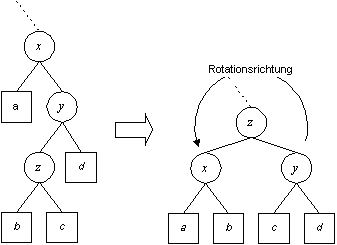

Entfernen in AVL-Bäumen
Auch das Entfernen von Elementen kann die AVL-Ausgeglichenheit verletzen. Umstrukturierungen können hierbei zu umfangreicheren Manipulationen führen.
Wie beim Einfügen werden die Balancefaktoren der einzelnen Knoten überprüft und im Falle von Abweichungen entsprechende Umstrukturierungen vorgenommen.
Ein (a, b)-Baum ist ein Baum mit folgenden Eigenschaften:
Die Elemente werden in den Blättern aufsteigend von links nach rechts gespeichert. Die Suche entspricht vom Aufwand her betrachtet der Suche in AVL-Bäumen, die Baumhöhe ist allgemein etwas geringer als bei AVL-Bäumen.
Beispiel: Suchen in einem (a, b)-Baum
IsIn(x, T)
Beispiel: (2, 4)-Baum
![]()
![]()
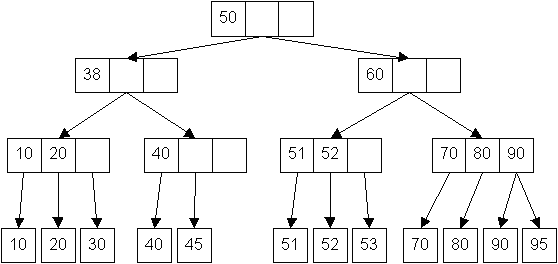
Ist es notwendig, Daten aus dem Hauptspeicher auszulagern - so hat die Erfahrung gezeigt - daß die Reproduktion der Strukturen von AVL-Bäumen in externen Medien keine optimale Lösung darstellt. Das Problem stellen hierbei insbesondere Zugriffe in den Hintergrundspeicher dar, also jene Zugriffe auf Daten, die zunächst nicht im Hauptspeicher gehalten werden. Offensichtlich bieten (a, b)-Bäume hier Möglichkeiten zur Realsierung für diverse Operationen, die unter diesen Bedingungen leistungsfähiger sind.
Das Streichen und Rebalancieren eines Blattes w als Sohn von v in einem Baum läßt sich wie folgt vornehmen:
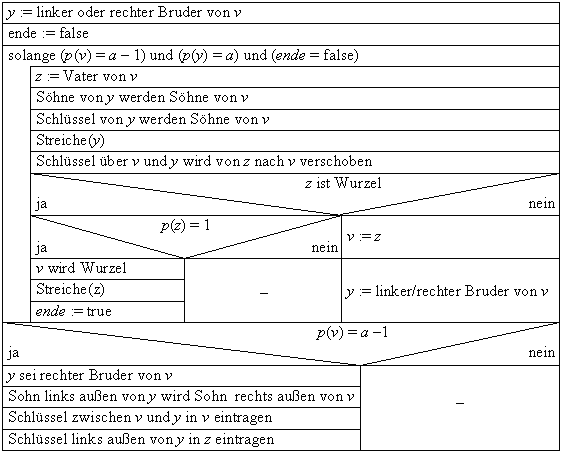
Balancierte Bäume sind allgemein dadurch charakterisiert, daß für jeden Knoten p dessen linker und rechter Teilbaum nicht zu unterschiedliche Größen aufweisen dürfen, bei AVL-Bäumen etwa, darf die Differenz nur im Intervall [-1 .. 1] Î N liegen. Die Definition verhindert zwar einseitige Entartungen wie etwa folgende Linearisierung:
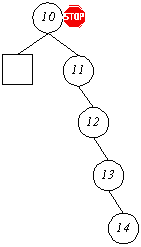
Beidseitige Entartungen wie diese
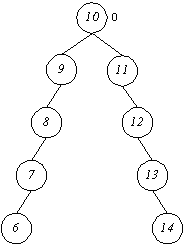
werden allerdings nicht wirksam verhindert, denn es werden beim Berechnen der Balancen nur Teilbäume einbezogen, die tatsächlich vorhanden sind - ein Knoten, von dem nur ein Teilbaum abgeht wird hierbei nicht betrachtet, da keine sinnvolle Differenz gebildet werden kann.
Das, was eigentlich verhindert werden soll, nämlich, daß sich die Sucheffizienz verschlechtert wird, da Listen- statt Baumstrukturen vorliegen, ist nun nachteiligerweise doch wieder möglich. Kurzum: Während die Strategie der Höhenbalancierung zunächst versucht einseitige Höhenentgleisungen zu nivellieren, versucht die Gewichtsbalancierung die Höhe an sich zu minimieren und die Effizienz von Suchoperationen durch möglichst viele sinnvolle Verzweigungen zu optimieren.
Die Forderung, die gewichtsbalancierte Bäumen nun erfüllen müssen, ist nicht mehr, eine Höhendifferenz der Teilbäume nicht zu überschreiten, sondern je Knoten p eine Differenz der Knotenanzahl in den Teilbäumen nicht zu übersteigen.
Folgendes Werkzeug wird zur Gewichtsbalancierung benötigt:
T:
Baum
Tl:linker Teilbaum
W(T) (auch als | T | notiert):Anzahl der Blätter des Baumes T
*
W(Tl) (auch als | Tl | notiert):Anzahl der Blätter des linken Teilbaumes Tl
*
p(T):Wurzelbalance
(Anstelle von 'Anzahl der Blätter' wird häufig auch der Ausdruck Gewicht benutzt)
Die Wurzelbalance p(T) ergibt sich als Quotient aus W(Tl) und W(T):
An jedem inneren Knoten p wird eine entsprechende Größe p(T) geführt:

Der oberste Knoten mit dem Schlüssel 5 bekommt also das Gewicht 5/8, denn der linke Teilbaum dieses Knotens umfaßt 5 Blätter, von diesem Knoten lassen sich darüber hinaus weitere 3 Blätter (also insgesamt 8 Blätter) erreichen, folgt noch aus den beiden Zahlen einen Quotienten zu bilden, fertig. Diese Berechnung wird an allen Knoten durchgeführt und nach jeder Einfüge/Entferne-Operation aktualisiert.
Eigenschaften der Wurzelbalance
Die Wurzelbalance muß korrekterweise innerhalb bestimmter Grenzen liegen, die sich mit einer Zahl a mit 0 £ a £ ½ umschreiben lassen. Man spricht von einem Suchbaum mit beschränkter Balance a oder von gewichtsbalanciert mit Balance a , kurz BB[a ]-Baum, wenn für jeden Teilbaum T ‘ von T gilt:
a £ p(T‘) £ (1 - a)
Einfacher gesagt, befinden sich korrekte Wurzelbalancen im Intervall [a, 1 - a], also etwa [0.25, 0.75]. Je näher sich die Werte für a an 0.5 befinden, je ausgeglichener verhalten sich die Teilbäume zueinander.
Wird a genau ½
gewählt, liegt ein optimaler Baum vor.
Aber ... ![]()
Was heißt das?
... Bedenkzeit ...
Nichts anderes, als daß das Intervall zulässiger Werte bei [0.5, 1 - 0.5] liegt, also genau [0.5, 0.5] ist, es ist somit nur ein Wert zulässig, 0.5, und Strukturen, wie diese asymmetrische hier ...
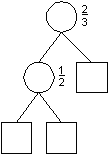
... sind nicht mehr in der Menge der gültigen Figuren. Jede zweite Einfügeoperation erzeugt aber eine automatisch eine solche asymmetrische (Teil-) Figur, zu starke Einschränkungen in dieser Hinsicht können also den sinnvollen Einsatz gewichtsbalancierter Bäume verhindern.
Suchen
Auch bei gewichtsbalancierten Bäumen wird ganz herkömmlich binärbaum-mäßig gesucht, der allgemeine oben angegebene Algorithmus gilt uneingeschränkt.
Einfügen
Auch hier wird zunächst das einzufügende Element gesucht und im Falle, daß es nicht gefunden wurde, an der Stelle - mit zwei Blättern/Söhnen - eingefügt, an der die Suche geendet hat.
Nun wird den Suchpfad zurückgegangen und geprüft, ob die Wurzelbalance an den Knoten auf diesem Weg innerhalb des gewünschten [a, 1 - a] liegt. Verlassen die Balancen die gewünschten Bereiche, werden Rotationen/Doppelrotationen durchgeführt, bis der Baum ausgeglichen ist.
Gewichtete Bäume schleppen - wie balancierte Bäume - nach bestimmten Kriterien berechnete Werte an den Knoten und Blättern mit sich. Der Unterschied besteht in der Art der Berechnung der entsprechenden Werte. Bei gewichteten Bäumen handelt es sich bei diesen Werten um Wahrscheinlichkeiten.
Beispiel: vier Informationen sind anhand vierer Schlüssel in einem gewichteten Baum unterzubringen.
Für die vier Schlüssel gilt, daß sie (bzw. die enthaltenen Informationen) mit abnehmenden Wahrscheinlichkeiten x1 < x2 < x3 < x4 benötigt werden.
Die Wahrscheinlichkeiten sind gegeben mit
w(> x1)
= 1/6
(= 4/24)
w(x1)= 1/24 (= 1/24)
w(x1, x2 )= 0
(= 0/24)
w(x2)= 1/8
(= 3/24)
w(x2, x3 )= 0
(= 0/24)
w(x3)= 1/8
(= 4/24)
w(x3, x4 )= 1/8
(= 0/24)
w(x4)
= 0
(= 0/24)
w(x4)
= 5/12 (= 10/24)
(ergibt eine Summe von 24/24)
Der entstehende Baum für
(a0, b1, a1, b2, a2, b3, a3, b4, a4)
mit
(1/6, 1/24, 0, 1/8, 0 ,1/8, 1/8, 0, 5/12)
ist wie folgt belegt:
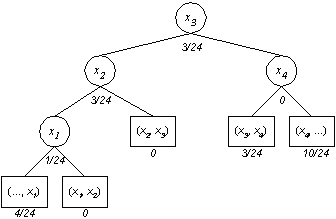
Da es sich hierbei um Wahrscheinlichkeiten handelt gilt für (a0, b1, a1, ... , bn, an), daß die Summe dieser Werte = 1 ist:
![]()
Hierzu einige Begriffe, in einem Suchbaum T für die Schlüsselmenge S bezeichnet man mit
biT die Tiefe des Knotens xi
ajT die Tiefe des Blattes (xj, xj+1), also z.B. a0T = 3 und a3T = 2
und mit PT die gewichtete Pfadlänge, die sich wie folgt ergibt
Die gewichtete Pfadlänge ist hierbei von Bedeutung, da die mittlere Suchzeit in einem gewichteten Baum proportional zu PT ist.
Für den Beispielbaum ergibt sich
b1T = 2
b2T = 1
b3T = 0
b4T = 1a0T = 3
a1T = 3
a2T = 2
a3T = 2
a4T = 2
sowie die bekannten
b1 = 1/24
b2 = 1/8
b3 = 1/8
b4 = 0a0 = 1/6
a1 = 0
a2 = 0
a3 = 1/8
a4 = 5/12
Somit ist PT = 1/24 × 3 + 1/8 × 2 + 1/8 × 1 + 0 × 2+ 1/6 × 3 + 0 × 3 + 0 × 2 + 1/8 × 2 + 5/12 × 2
= 1/8 + 2/8 + 1/8 + 1/2 + 1/4 + 5/6
= 2 1/12
Bisher wurden in Rahmen unserer Veranstaltung Programme lediglich getestet, um Fehler zu finden. Hierbei tritt jedoch das Problem auf, das nur besagt werden kann, welche Fehler ein Programm zu einem Zeitpunkt noch hatte (eben weil sie gefunden wurden). Wird kein Fehler gefunden, ist keineswegs das Programm mit Sicherheit fehlerfrei, sondern es wurde lediglich kein Fehler gefunden - das ist etwas grundlegend anderes.
Die nun vorgestellte Methode beansprucht für sich, direkt zu beweisen, daß ein Programm fehlerfrei ist.
Man unterscheidet generell zwischen totaler Korrektheit und partieller Korrektheit, wobei der Unterschied in der Terminierung des Programmstückes liegt. Schließt P die sichere Terminierung mit ein, spricht man bei erfolgtem Beweis von einem total korrekten Programmteil, andernfalls nur von partieller Korrektheit. Kann zunächst lediglich der Beweis partieller Korrektheit erbracht werden, gibt es die Möglichkeit, Terminierungsbeweise separat zu führen.
Die Verifikation funktioniert anhand von logischen Ausdrücken, sogenannten Zusicherungen, die um die Programmteile herum angebracht werden. Der Ansatz bei dieser Technik sind die Zustände eines Programms - also die jeweiligen Werte der enthaltenen Variablen.
Man notiert sich hierbei Voraussetzungen P, unter denen eine Operation ausgeführt wird, die Anweisung V selbst und das - unter der Erfullung der Voraussetzungen - sichere Ergebnis Q. Allgemein bezeichnet die Literatur P als Vorbedingung und Q als Nachbedingung. Von außen besehen entsteht also Code in Gestalt sogenannter Hoare-Tripel:
{ P }
V
{ Q }
Vor- und Nachbedinungen werden meist in geschweiften Klammern angegeben und in Form von Kommentaren in den Quelltext eingefügt.
Beispiel
Das folgende Stück Code ermittelt den Rest einer ganzzahligen Division mit Eingaben für x und y >= 0. Teilt man etwa 25 durch 4 mit dem Aufruf rest(25, 4) paßt dies 6 mal (6 × 4 = 24), der Rest 1 bleibt übrig. Diese Reste ermittelt die Routine:
function rest (x : integer; y : integer) : integer;
var q, r : integer;
begin
...
q := 0;
r := x;
while r >= y do
begin
r := r - y;
q := q + 1;
end;
...
end;
Das Prinzip ist, solange von der größeren Zahl den Divisor abzuziehen, bis das Ergebnis kleiner als der Divisor ist, dies ist der Rest.
Es ergibt sich ganz allgemein folgendes Hoare-Tripel:
{P: x ³ 0 Ù y > 0}
Routine rest
{Q: x = q × y + r Ù r ³ 0 Ù r < y}
Unter der Bedingung gültiger Eingaben, ergibt sich also eine Konstellation der Zahlen, in der x aus der Eingabe y und Anzahl der Divisionen q sowie dem Rest rekonstruierbar ist und in der 0 £ r < y gilt (r kann minmal 0 sein und maximal y - 1 sein, anderfalls wäre r kein richtiger Rest).
![]() Die Verifikation wird von hinten nach
vorne durchgeführt, zielorientiert also.
Die Verifikation wird von hinten nach
vorne durchgeführt, zielorientiert also.
Zunächst bilden sich vier Abschnitte v1, v2, v3 und v4 heraus:

Dann beginnt die mathematische Seite dieses Fachs ...
(I) Es gilt für den Abschnitt v1:
{ x = q × y + r }
v1
{ x = q × y + r }Begründung: Vor Ausführung gilt
x = q × y + r
Danach gilt

= (q + 1) × y + r - y (Anweisungen in v1)
also
= (qy + y) + r - y (umformen)



= q × y + r
(II) Für den Abschnitt v2 gilt:
{ x = q × y + r Ù r ³ 0 }
v2
{ x = q × y + r Ù r ³ 0 Ù r < y}Begründung: Vor Ausführung gilt
x = q × y + r Ù r ³ 0
Danach gilt


= q × y + r (folgt aus (I))
Da die Schleife nur ausgeführt wird, wenn r ³ y ist, kann r im Schritt r := r - y; nicht kleiner 0 werden, wenn am Anfang r ³ 0 erfüllt war, daher gilt r ³ 0 nach v2. Ist hingegen r > y kommt die Schleife nicht mehr zur Ausführung. Bis dieser Zustand eingetreten ist, wird die Schleife allerdings durchlaufen, daher gilt auch r < y nach v2.
(III) Für Abschnitt v3 gilt:
{ x ³ 0 Ù y > 0 }
v3
{ x = q × y + r Ù r ³ 0}Begründung: Vor Ausführung gilt
x ³ 0 Ù y > 0
Danach gilt


x = 0 × y + x
Dies folgt aus der Belegung von q mit 0 und von r mit x.
(IV) und für v4 gilt:
{ x ³ 0 Ù y > 0 }
v3
{ x = q × y + r Ù r ³ 0 Ù r < y}Dies folgt direkt aus (II) und (III).
![]() Da das Beweisen von Programmen eine kompliziertere
Angelegenheit ist, gebietet die Praxis nicht erst ein
langes Programm einzugeben und dann 'durchzubeweisen', sondern
Programm und Beweis Hand in Hand zu entwickeln und entsprechend
gradlinig zum einfachen Beweisen zu implementieren.
Da das Beweisen von Programmen eine kompliziertere
Angelegenheit ist, gebietet die Praxis nicht erst ein
langes Programm einzugeben und dann 'durchzubeweisen', sondern
Programm und Beweis Hand in Hand zu entwickeln und entsprechend
gradlinig zum einfachen Beweisen zu implementieren.
Wie eine Verifikation aussieht, ist nun offensichtlich. Keine Macht der Welt kann uns nunmehr vor doppelt so langen Sourcecodes retten. Was ist im einzelnen aber geschehen?
Ähnlich wie bei Beweisen mit vollständiger Induktion gibt es einige feste Regeln, anhand derer in den einzelnen Programmkonstrukten verfahren werden kann.
R1: Anweisungsfolgen (Regel der sequentiellen Komposition)
{ P } S1
{ Q }; { Q } S2
{ R }
![]()
{ P } S1;
S2 { R }![]()
Wenn S1 Variablen von einem Zustand s nach den Vorbedingungen P aus in einen Zustand s ' versetzt in dem die Nachbedingungen Q gültig sind, und S2 von einem Q-Zustand s' in einen R-Zustand s'' führt, dann führt die Nacheinandderausführung von S1 und S2 auch s nach s''.
Beispiel:
Unser Beispielprogramm enthält die Folge einfacher Anweisungen
r := r - y;
q := q + 1;
Hier kann gemäß der Regel für Anweisungsfolgen zeilenweise vorgegangen werden ...
{ x = y × (q + 1) + r - y }
r := r - y;
{ x = y × (q + 1) + r }
q := q + 1;
{ x = y × q + r }
... oder umfassender:
{ x = y × (q + 1) + r - y }
r := r - y;
q := q + 1;
{ x = y × q + r }
R2: Zuweisungen (Zuweisungsaxiom, Regel für Ergibt-Anweisungen)
{ PEx } x := E { P }
Hierbei bedeutet PEx, daß x durch E substituiert werden muß, damit die Nachbedingung P wahr wird. Dies fordert gelegentlich weitere logische Überlegungen, etwa:
{ x + 1 > a }
x := x + 1;
{ x > a }
R3: Regel der Fallunterscheidung
{ P Ù B } S1
{ R }
{ P Ù ØB } S2 {
R }
![]()
if B
then
S1 else S2![]()
R4: Regel der Iteration
{ P Ù I } S
{ I }
![]()
{ I } while
P do S end![]() { ØP Ù I }
{ ØP Ù I }
P wird als Invariante der Schleife bezeichnet, sie muß am Anfang und am Ende des Schleifenrumpfs gelten.
R5: Regel der Wiederholung
{ P } S
{ Q }, { Q Ù ØB
}
![]()
{ P } repeat
S until![]() B { Q Ù B
}
B { Q Ù B
}
Verifikation von Anweisungen zum Vertauschen zweier Variablen
x := x + y;
y := x - y;
x := x - y;
1. Zunächst sollten die Beweisziele und -voraussetzungen dargelegt werden, d. h. Vor- und Nachbedingungen sind einzutragen (man sollte hierbei wissen, was man wollte, strenggenommen gibt es nämlich keine falschen Programme, sondern nur eine Vielzahl, die sich anders verhält, als die Entwickler dachten):
{ x = A Ù y = B}
x := x + y;
y := x - y;
x := x - y;
{ y = A Ù x = B}Das heißt, x befindet sich anfangs in einem Zustand A, y in einem Zustand B, nach Ausführung der Anweisungsfolge soll sich y im Zustand A befinden und x im Zustand B.
2. Gemäß Zuweisungsaxiom { PxE } x := E { P } von unten her die rechten Seiten (die 'E's) substituieren:
{ x = A Ù y = B}
x := x + y;
y := x - y;
{ y = A Ù x - y = B}/
Pxx - y
x := x - y;
{ y = A Ù x = B}Der Zustand der Variablen x wird durch x - y hervorgerufen.
{ x = A Ù y = B}
x := x + y;
{ x - y = A Ù x - (x - y) = B}/
Pyx - y
y := x - y;
{ y = A Ù x - y = B}
x := x - y;
{ y = A Ù x = B}
Und dasselbe erneut, y ergibt sich aus x - y, entsprechend ist dieser Term in den Zustandsbeschreibungen (immer nach oben hin!) einfach zu substituieren.
{ (x + y) - y = A Ù (x + y) - ((x + y) - y) = B}
/
Pxx + y
x := x + y;
{ x - y = A Ù x - (x - y) = B}
y := x - y;
{ y = A Ù x - y = B}
x := x - y;
{ y = A Ù x = B}
Und wieder: x wird durch x + y nach oben hin ersetzt.
3. (Wenn nötig) Terme vereinfachen:
{ x + y - y = A Ù x + y -x - y + y = B
Û
x = A Ù y = B }Dann ergibt sich insgesamt:
{ x = A Ù y = B}
x := x + y;
{ x - y = A Ù x - (x - y) = B}
y := x - y;
{ y = A Ù x - y = B}
x := x - y;
{ y = A Ù x = B}
Verifikation einer Multiplikation durch Aufsummierung
Die hier durchgeführte Multiplikation für z = x × y ist nichts anderes als die x-malige Aufsummierung von y, also z = y + y + y + ... (x-mal)
x := A;
y := B;
z := 0;
u := 0;
while u <> x do
begin
z := z + y;
u := u + 1;
end;
1. Vor- und Nachbedingungen des gesamten Programmteils festlegen:
x := A;
y := B;
{ ab hier, das darüber ist lediglich die Vorbelegung der Variablen}{ x = A Ù y = B }
u := 0;
z := 0;
while u <> x do
begin
z := z + y;
u := u + 1;
end;
{ z =}
{ z = A × B }
2. Von unten nach oben anhand der Hoare-Regeln voranarbeiten, zunächst also die While-Schleife erledigen. Problem hierbei: Es muß eine eine für die Schleife relevante Bedingung I gefunden werden, die am Anfang und am Ende des Schleifenrumpfes gilt, eine sogenannte Invariante, dies ist erfahrungsgemäß nicht trivial. Eine solche Zusicherung kann in dem Ausdruck
z = ![]() Ù u £ x
Ù u £ x
gefunden werden. Die Variable z ist zu jedem Zeitpunkt die Summe der bis dato gestappelten y, und u ist niemals größer als x.
x := A;
y := B;
{ x = A Ù y = B }
u := 0;
z := 0;
{ x = A Ù y = B Ù u = 0 Ù z =}
while u <> x do
begin
z := z + y;
u := u + 1;
end;
{ x = A Ù y = B Ù u = x Ù z =}
{ z =}
{ z = A × B }
Nun bleiben noch die beiden Zuweisungen innerhalb der While-Schleife, die wie im ersten Beispiel einfach nach oben substituiert werden. In der unteren Zeile geschieht dies implizit durch Verändern der Relation von £ zu ¹ (von unten nach oben) und direkt durch Verstellen der Obergrenze im Summenzeichen.
x := A;
y := B;
{ x = A Ù y = B }
u := 0;
z := 0;
{ x = A Ù y = B Ù u = 0 Ù z =}
while u <> x do
begin
{ x = A Ù y = B Ù u ¹ x Ù z + y =
}
z := z + y;
{ x = A Ù y = B Ù u ¹ x Ù z =
}
{ x = A Ù y = B Ù u ¹ x Ù z =
}
u := u + 1;
{ x = A Ù y = B Ù u £ x Ù z =
}
end;
{ x = A Ù y = B Ù u = x Ù z =}
{ z =}
{ z = A × B }
Damit ist auch dieser ehedem kurze Quelltext durchzogen mit Hoare-Klauseln und anstelle von 9 Zeilen sind nun genau 18 Zeilen lang zu scrollen.
Verifikation einer linearen Suche
Das folgende Stück Code sucht ein Element x in einem Feld a mit n Elementen, indem von vorne bis hinten durch das Feld gegangen (siehe Suchen in geordneten Mengen) und das aktuelle Element mit x verglichen wird:
i := 1;
while a[i] <> x do
begin
i := i + 1;
end;
1. Aufstellen der umfassenden Vor- und Nachbedingungen:
{ x Î a[1..n] }
i := 1;
while a[i] <> x do
begin
i := i + 1;
end;
{ a[i] = x }
2. Anhand der Hoare-Regeln von unten nach oben durch den Code gehen.
Dies beginnt auch hier wieder mit einer While-Schleife, für die eine Invariante zu finden ist. Dafür läßt sich eine Ableitung der Vorbedingung einspannen: x Î a[i..n]. Damit ergeben sich folgende Hoare-Klauseln:
{ x Î a[1..n] }
i := 1;
{ x Î a[i..n] }
while a[i] <> x do
begin
{ x Î a[i..n] Ù x ¹ a[i]}
i := i + 1;
end;
{ x Î a[i..n] Ù a[i..n] = x}
{ a[i] = x }
Bleibt noch die Zuweisung innerhalb der Schleife (die Zuweisung am Anfang hat sich zwischen der Invarianten und der Vorbedingung makellos selbst bewiesen):
{ x Î a[1..n] }
i := 1;
{ x Î a[i..n] }
while a[i] <> x do
begin
{ x Î a[i..n] Ù x ¹ a[i] }
{ x Î a[i + 1..n] }
i := i + 1;
{ x Î a[i..n] }
end;
{ x Î a[i..n] }
{ a[i] = x }
Verifikation von Code zur Ermittlung des ggT
Der folgende Code zieht jeweils die Variable mit dem aktuell größeren Wert von der mit dem momentan kleineren Wert ab. Dies wird wiederholt, bis beide Variablen den gleichen Wert haben, ist dies erreicht, ist der ggT ermittelt.
{ x > 0 Ù y > 0 }
a := x;
b := y;
repeat
while a > b do
a := a - b;
while b > a do
b := b - a;
until a = b
{ a = b Ù b = ggT(x, y) }
1. Aufstellen der umfassenden Vor- und Nachbedingungen:
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;
b := y;
repeat
while a > b do
a := a - b;
while b > a do
b := b - a;
until a = b
{ a = b Ù b = ggT(x, y) }
2. Bilden der restlichen Hoare-Tripel:
2.1 Mit dem Zuweisungsaxiom den Inhalt der unteren While-Schleife festlegen:
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;
b := y;
repeat
while a > b do
a := a - b;
while b > a do
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
b := b - a;
/
Pbb - a
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
until a = b
{ a = b Ù b = ggT(x, y) }
2.2 Anhand der Iterationsregel die untere
While-Schleife belegen
![]()
![]() (Invariante: {
a > 0 Ù b
> 0 Ù ggT(x, y) = ggT(a, b) Ù (b
> a) }):
(Invariante: {
a > 0 Ù b
> 0 Ù ggT(x, y) = ggT(a, b) Ù (b
> a) }):
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;
b := y;
repeat
while a > b do
a := a - b;
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) Ù (b > a) }
while b > a do
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) Ù (b > a) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
b := b - a;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) Ù Ø(b > a) }
until a = b
{ a = b Ù b = ggT(x, y) }
2.3. Mit dem Zuweisungsaxiom den Inhalt der oberen While-Schleife festlegen:
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;
b := y;
repeat
while a > b do
{ a - b > 0 Ù b > 0 Ù ggT(x, y) = ggT(a - b, b) }
a := a - b;
/
Paa - b
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) Ù (b > a) }
while b > a do
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) Ù (b > a) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
b := b - a;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) Ù Ø(b > a) }
until a = b
{ a = b Ù b = ggT(x, y) }
2.4 Anhand der Iterationsregel die obere
While-Schleife belegen
![]()
![]() (Invariante: {
a > 0 Ù b
> 0 Ù ggT(x, y) = ggT(a, b) Ù (a
> b) }):
(Invariante: {
a > 0 Ù b
> 0 Ù ggT(x, y) = ggT(a, b) Ù (a
> b) }):
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;
b := y;
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) }
repeat
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
while a > b do
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
{ a - b > 0 Ù b > 0 Ù ggT(x, y) = ggT(a - b, b) }
a := a - b;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø (a > b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
while b > a do
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
b := b - a;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø(b > a) }
until a = b
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù a = b }
{ a = b Ù b = ggT(x, y) }
2.5. Die Repeat-Schleife ...
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;
b := y;
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) }
repeat
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
while a > b do
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
{ a - b > 0 Ù b > 0 Ù ggT(x, y) = ggT(a - b, b) }
a := a - b;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø (a > b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
while b > a do
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
b := b - a;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø(b > a) }
until a = b
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù a = b }
{ a = b Ù b = ggT(x, y) }
2.6 Und zuletzt die Zuweisungen am Anfang des Programms mit der Zuweisungsregel verifizieren:
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;/
Pxa
{ a > 0 Ù y > 0 Ù ggT(a, y) }
b := y;/
Pyb
{ a > 0 Ù b > 0 Ù ggT(a, b) }
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) }
repeat
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
while a > b do
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
{ a - b > 0 Ù b > 0 Ù ggT(x, y) = ggT(a - b, b) }
a := a - b;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø (a > b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
while b > a do
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
b := b - a;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø(b > a) }
until a = b
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù a = b }
{ a = b Ù b = ggT(x, y) }
2.6(a) Die Zuweisungen lassen sich mittels der Regel der sequentiellen Komposition auch zu einem Verifikationsschritt zusammenfassen:
{ x > 0 Ù y > 0 Ù ggT(x, y) }
a := x;/
Pxa
b := y;/
Pyb
{ a > 0 Ù b > 0 Ù ggT(a, b) }
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) }
repeat
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
while a > b do
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (a > b) }
{ a - b > 0 Ù b > 0 Ù ggT(x, y) = ggT(a - b, b) }
a := a - b;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø (a > b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
while b > a do
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b) Ù (b > a) }
{ a > 0 Ù b - a > 0 Ù ggT(x, y) = ggT(a, b - a) }
b := b - a;
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) }
{ a > 0 Ù b > 0 Ù ggT(x, y) = ggT(a, b) Ù Ø(b > a) }
until a = b
{ a > 0 Ù b> 0 Ù ggT(x, y) = ggT(a, b) Ù a = b }
{ a = b Ù b = ggT(x, y) }
Verifikation von Code zur Berechnung der Fakultät einer Zahl
Dieser Code multipliziert eine aufsteigende Folge natürlicher Zahlen von 2 bis N und speichert das jeweilige Ergebnis in der Variablen z. Nach Terminierung des Codefragments, bleibt die Fakultät von N in z erhalten.
i := N;
z := 1;
u := 1;
while (u <> i) do
begin
z := z * (u + 1);
u := u + 1;
end;
1. Festlegen der Vor- und Nachbedingungen
{ N > 0 }
i := N;
z := 1;
u := 1;
while (u <> i) do
begin
z := z * (u + 1);
u := u + 1;
end;
{ i > 0 Ù z = N!}
![]()
Wichtiger Hinweis: Falls Inhalte von Verweisen (Links) nicht angezeigt werden, könnte das an einer falschen Konfigurierung des Zielservers liegen. Versuchen Sie dann mit Rechtsklick und Öffnen im neuen Fenster bzw. Register dort in der Adresszeile zu Beginn das angegebene Protokoll (https://) in die unsichere Variante (http://) zu ändern und den Link so aufzurufen.
Sortieren
https://www-lehre.informatik.uni-osnabrueck.de/~ainf/skript/node42.html
Verifikation
https://www.informatik.hu-berlin.de/~roch/Studium/verifik.html
Jan Ebert: Beispielverifikation mit dem HOARE'schen Kalkül (Postscript)
Gregor Engelmeier: Programmverifikation "Schritt für Schritt" (Postscript)
Ralf Kruber: Ausgewählte Beispiele zum Hoare-Kalkül (Postscript)
Hinweise, Korrekturen und Ergänzungen können an Michael Gellner gerichtet werden.