Aufgabe:
Es soll ein Projekt StackCalc konzipiert werden, das mit beliebig langen, ganzen Zahlen rechnet, wobei im Ergebnis alle signifikanten Ziffern erhalten bleiben. Die Langzahlen werden in Stapeln (Attribute der Klasse StackCalc) abgelegt, nur einzelne Grundrechenarten (Addition, Multiplikation) und Grundmethoden (Schreiben einer Langzahl, also String-Rückgabe aus Stapel) sind zu entwickeln sowie eine Consolen-Test-Klasse ConStackCalc, mit deren Hilfe einzelne Rechnungen angewiesen und Ergebnisse angezeigt werden.
Die Abbildung rechts zeigt mögliche Ausgaben auf der Console durch Anklicken auch groß.
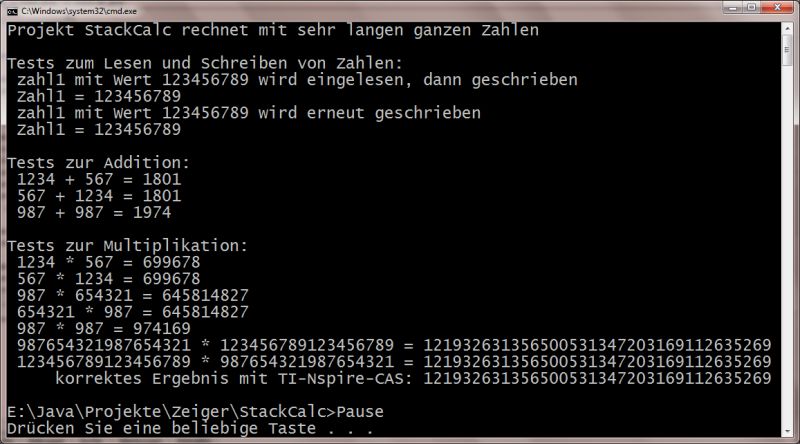
a) Laden Sie die bereits fertigen Klassen ConStackCalc und Stack (Stand Zentral-Abitur 2012) und eine Rumpf-Klasse StackCalc (als Version v0.8), speichern Sie diese im eigenen Ordner (z. B. StackCalc), studieren Sie die Klassen und ergänzen Sie in StackCalc die interne Methode _write(), die eine im Stapel abgelegte Langzahl als String zurückgibt für die Anzeige. Testen Sie, dass nun der erste Testteil (Tests zum Lesen und Schreiben von Zahlen) korrekt auf der Konsole angezeigt wird.
b) Beschreiben Sie in Form eines UML-Beziehungs-Diagramms (auch Implementierungs-Diagramm genannt) alle vier Klassen (ConStackCalc, StackCalc, Stack und Node) und die Beziehungen zwischen ihnen und ihren Objekten. Kontrollieren Sie Ihr Diagramm anschließend mit der nebenstehenden Abbildung (Klick darauf zeigt das Diagramm groß). Diskutieren Sie, ob Assoziationen oder besser Kompositionen angemessen sind.
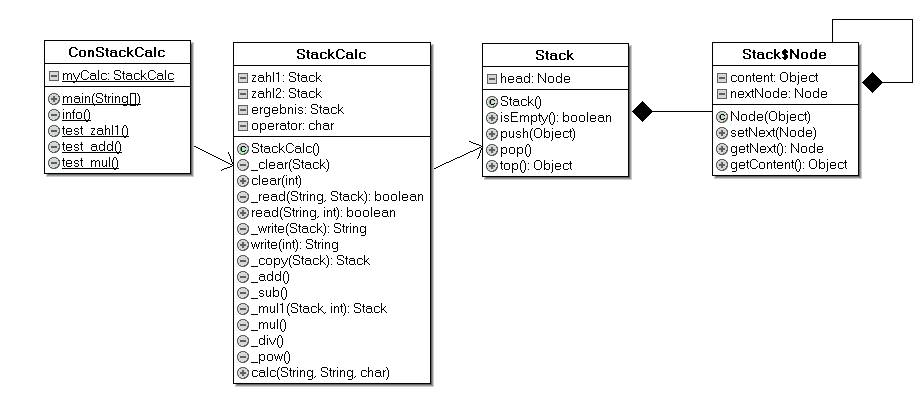
c) Kopieren Sie die drei Klassendateien in ein Unter-Verzeichnis (z. B. StackCalc/v08) und laden Sie die nächste Datei-Generation der StackCalc-Klasse (Version v0.9) in den Hauptordner (z. B. StackCalc). Hierin ist die Methode _write() fertig implementiert. Vergleichen Sie mit Ihrer Implementierung.
Ergänzen Sie in Version v0.9 nun die interne, private Methode _add(), die von der öffentlichen Methode calc() aufgerufen wird. Nach der Fertigstellung speichern Sie auch diese Klassendatei StackCalc.java gemeinsam mit Stack und ConStackCalc in einem neuen Unterverzeichnis StackCalc/v09 ab.
d) Sichern Sie Ihre fertige Version StackCalc v0.9 wie beschrieben, laden Sie die neue Version v1.0 von StackCalc in den Hauptordner (z. B. StackCalc). Hier ist die interne Methode _add() fertig implementiert, möglicherweise anders als in Ihrer Lösung. Vergleichen Sie beide Lösungen.
Ergänzen Sie in Version v1.0 nun die interne, private Methode _mul(), die von der öffentlichen Methode calc() aufgerufen wird und die Multiplikation zweier als Stapel gespeicherter Zahlen realisiert. Notieren Sie sich zur Vorbereitung einige schriftliche Multiplikationen (z. B. 1234*567 oder 567*1234 oder 789*789) und überlegen Sie, wie dies in einem Algorithmus ablaufen könnte. Notieren Sie einen Grobalgorithmus und/ oder zeichnen Sie zu _mul() ein Struktogramm.
Tipps: Zur Bildung der Zwischensummen nach Fertigstellung jeder Teil-Multiplikation mit einer (der jeweils letzten?) Ziffer der zweiten (Rest-)zahl kann ggf. die interne, bereits fertige Methode _add() genutzt werden, natürlich nach vorheriger Bereitstellung der beiden Summanden in den Zahlstapeln und abschließender Restaurierung der Stapel mit den ursprünglichen Faktoren.
Testen Sie ausgiebig Ihre Lösung mit Hilfe der Testumgebung ConStackCalc. Beachten Sie insbesondere, ob bei ungleich langen Zahlen alle Ziffern genutzt und alle Überträge berücksichtigt werden. Nach der Fertigstellung speichern Sie auch diese Klassendatei StackCalc.java gemeinsam mit Stack und ConStackCalc in einem neuen Unterverzeichnis v10 ab.
e) Abschließend könnten nun auch die internen Methoden _sub() und _div() ergänzt werden. Die Ganzzahl-Division liefert ggf. im Ergebnis einen Rest. So könnte als Ergebis von 14/3 im Stapel ergebnis 4-R-2 (2 oben) liegen. Bislang sind nur positive Operanden berücksichtigt. Prüfen Sie, auf welche Weise das Vorzeichen angemessen gespeichert und berücksichtigt werden kann.
Download (* nicht öffentlich)
-
Java-Klassen
[Stack und Node] (gem. NRW-Zentral-Abitur ab 2012)
StackCalc [v0.8] [v0.9] [v1.0] und fertige Testumgebung [ConStackCalc] - JavaEditor
- Struktogramm-Editor Vips
- [Aufgabe und Abbildungen] als PDF
Zu den Literaturlisten
Zurück zur Übersicht aller Unterrichtsmaterialien
Weitere Lösungen: (aber erst selbst bearbeiten!)