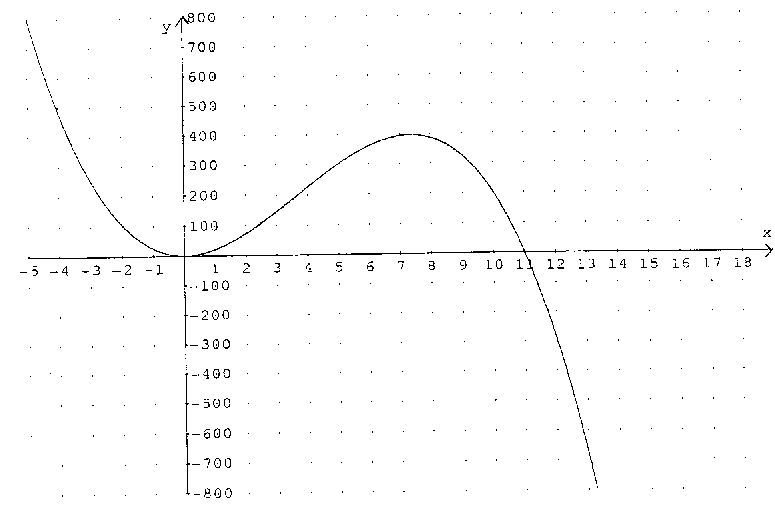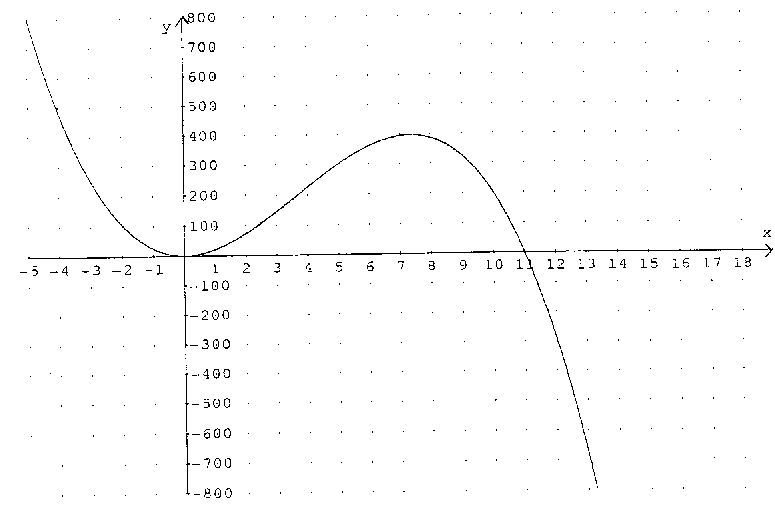Vergleichsarbeit Analysis Stufe 11

im 2. Halbjahr des Schuljahres 1999/2000

Vorgesehene Bearbeitungszeit: 2 Unterrichtsstunden

Name:_________________________________________

Kurs:__________________________________________

Allgemeine Vorbemerkungen:
Tragen Sie Ihren Namen und Ihren Kurs auf diesem Bogen ein.
Denken Sie daran, dass Sie diesen Aufgabenbogen mit Ihren übrigen Ausarbeitungen wieder abgeben, da sich auf ihm die Lösung der Teilaufgabe 2a) befinden.
Achten Sie auf Sauberkeit und Übersichtlichkeit Ihrer Darstellung.
Auch formale Mängel können zur Abwertung führen!

Aufgabe 1:

Eine Parabel hat eine Gleichung der Form f(x) = ax² + bx.

1. In A(3;3) hat sie die Steigung -2. Ermitteln Sie die Gleichung der Parabel.
   [Zur Kontrolle: f(x) = -x² + 4x ]
   
2. Ermitteln Sie für x₀ = 1 die Gleichung der Tangente an die Parabel. Wie groß ist der Winkel, den die Tangente mit der positiven Richtung der x-Achse bildet?
   
3. Stellen Sie die Gleichung der Normalen zur Tangente durch B(1; y₀) auf. Zeichnen Sie die Parabel, die Tangente und die Normale in dasselbe Koordinatensystem. Wählen Sie als Einheit auf beiden Achsen jeweils 1 cm.
   
4. Von einer Funktion g sei bekannt, dass für alle x die Beziehung g’(x) = f(x) gilt.
   

Untersuchen Sie den Graphen von g auf Wendestellen.

Aufgabe 2:

Das Bild auf der folgenden Seite zeigt den Graphen einer ganz-rationalen Funktion h.

Skizzieren Sie einen möglichen Graphen der Ableitung von h. Benutzen Sie dazu das Koordinatensystem, in welchem der Graph von h bereits eingetragen ist.


Die Funktion f mit f(x) = -2x³ + 24x² besitzt einen vergleichbaren Graphen wie h.
Zwischen ihren Nullstellen beschreibt die Funktion f die Wassermenge in einem Pumpspeicherwerk. Bestimmen Sie diesen Bereich. Dabei geben die y-Werte die Wassermenge in m³, die x-Werte (x³ 0) die Zeit in Stunden an.

1. Wann wird nach dem Zeitpunkt x=0 die maximale Wassermenge erreicht, wie groß ist dieser maximale Wasserbestand?
   
2. Was bedeuten im Zusammenhang mit dem in Aufgabenteil b) beschriebenen Sachverhalt die Begriffe mittlere Änderungsrate der Funktion f und lokale Änderungsrate der Funk-tion f?
   

   Bestimmen Sie den Wendepunkt des Graphen von f.
   

3. Welche Bedeutung hat die Wendestelle von f im Zusammenhang mit dem in Aufgabenteil b) beschriebenen Sachverhalt?
   

Vergleichsarbeit Analysis Stufe 11 , Seite 2

Name:____________________________________

Skizze zu Aufgabe 2:

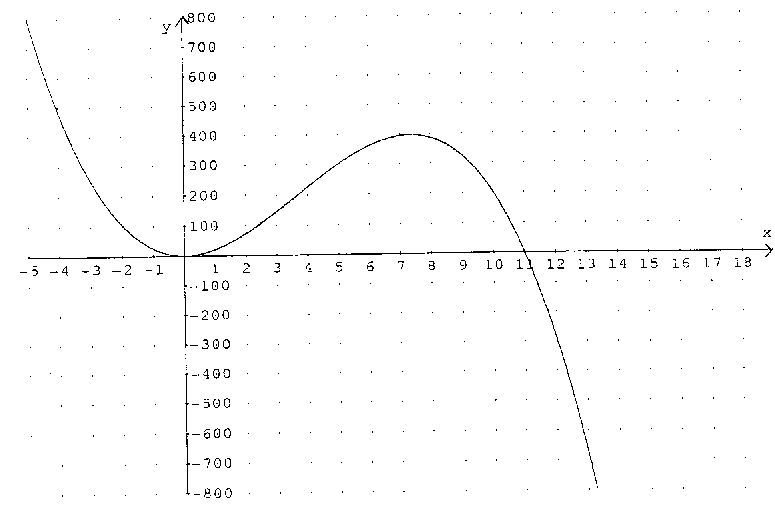
Aufgabe 3:

In der ebenen Geometrie ist eine Tangente an einen Kreis definiert als eine Gerade, die mit dem Kreis genau einen Punkt gemeinsam hat. Im Rahmen der Differentialrechnung wurde allgemein der Begriff der Tangente an den Graphen einer ganz-rationalen Funktion f im Punkt (x₀; f(x₀)) definiert.

1. Wie lautet diese Definition des Tangentenbegriffs in der Analysis?
   
2. Weisen Sie nach, dass eine Tangente an einen Funktionsgraphen durchaus mehr als einen gemeinsamen Punkt mit diesem Funktionsgraphen haben kann. Wählen Sie dazu als Beispielfunktion die Funktion f mit f(x) = x³- x² + 2. Stellen Sie die Gleichung der Tangente im Punkt (3; 20) auf, und berechnen Sie die gemeinsamen Punkte von Funktionsgraph und Tangente.
3. Bei Parabeln zweiter Ordnung vom Typ f(x) = ax² (a¹ 0) allerdings haben Graph und Tangente (im Sinne der Analysis-Definition gemäß Aufgabenteil a)) in einem Punkt P nur diesen Punkt P gemeinsam. Weisen Sie diesen Sachverhalt für den Punkt (2; 4a) nach.
   
4. Zeichnen Sie auf der Normalparabel zu y = x² einen vom Ursprung verschiedenen allgemeinen Punkt P=(p;p²) ein. Fällen sie von P das Lot auf die y-Achse und bezeichnen Sie den sich ergebenden Lotfußpunkt mit Q. Spiegeln Sie nun Q an der x-Achse. Als Spiegelpunkt erhalten Sie einen Punkt R. Weisen Sie nach, dass R der Schnittpunkt der y-Achse mit der Tangente an die Normalparabel im Punkt P ist.
   

Quelle: BezReg. Düsseldorf .:. Anpassungen: © 2004 Ziemke
Letzte Aktualisierung am 2. Januar 2004 durch den WebMaster.