Lösung der Aufgabe 1:
zu 1a)
Gegeben sind die Punkte
A(0/4), B(4/5), C(2/-3,5)
Mit f(x) = ax² + bx + c (allgemeine
Gleichung der quadratischen Funktion)
gilt: f(0) = 4, also c
= 4 und f(4) = 5, also 16a + 4b + c = 5
und f(2) = -3,5, also
4a + 2b + c = -3,5
als Lineares Gleichungssystem (LGS) notiert
und gelöst:
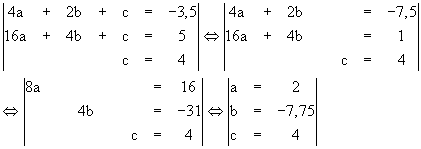
also ist f(x) = 2x² - 7,75x + 4
zu 1b)
Im Matrix-Editor (MATRIX
/ EDIT) werden die Dimension 3x4 und alle Koeffizienten des LGS
eingegeben:
[[4 2 1 -3,5][16 4 1 5][0 0 1 4]]
und die Lösungsmatrix
mit MATRIX / MATH / rref() erzeugt:
[[1 0 0 2][0 1 0 -7,75][0
0 1 4]]
Diese Lösungen stimmen mit den obigen Berechnungen
überein.
zu 1c)
Nach Eingabe des Funktionsterms
2x² - 7,75x + 4 im Y-Editor und Anpassung der Window-Einstellungen
( -1 <= x <= 5 und -5 <= y <= 10
) werden die Nullstellen z. B. mit CALC / zero() ermittelt: xN1 = 0,61
und xN2 = 3,26 .
Der Wertebereich hat als
untere Grenze das Minimum (y-Wert des Tiefpunktes), welches mit
CALC / minimum() ermittelt wird:
Minimum bei x = 1,94
mit y = -3,51 ;
also gilt für den Wertebereich:
W(f) = [ -3,51 ; +unendlich [