Einführungs-Aufgabe:
a) Interaktive Graphenverwandlung
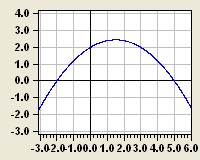
Ermitteln Sie zu nebenstehendem Graph die Funktionsgleichung
interaktiv sowohl in der Normalform als auch in der Scheitelpunktform.
Als Übung 3
steht im Lernportal hierzu ein interaktives Tabellenblatt mit den
entsprechenden Registern zur Verfügung.
Hinweis: Nur die Punkte P1(-2/0), P2(0/2) und P3(5/0) sind verlässlich bekannt.
b) Funktionsgleichung in Normalform algebraisch bilden
Nachdem zu den drei bekannten Punkten Funktionalgleichungen aufgestellt sind,
f(-2) = 0, also 4a - 2b + c = 0f(0) = 2, also c = 2
f(5) = 0, also 25a + 5b + c = 0
Gleichungen verbergen
werden diese als Lineares Gleichungssystem gelöst.
Allgemeine Funktionsgleichung:
f(x)
= ax² + bx + c
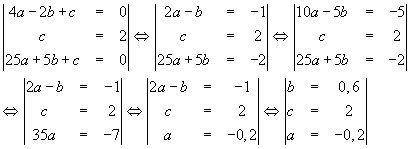
Also lautet die
Funktionsgleichung: f(x) = -0,2x² + 0,6x + 2
Eine Überprüfung
am Graph
-0,2x² - also gestaucht und nach unten geöffnet
... + 2 - also y-Achsenabschnitt bei -2
bestätigt das Ergebnis.
c) Funktionsgleichung in Scheitelpunktform wandeln
Durch Ausklammern des Koeffizienten vor x², ergänzen der quadratischen Ergänzung, Anwendung einer Binomischen Formel und Klammerauflösen wird der Term in die Scheitelpunktform gewandelt und die Koordinaten des Scheitelpunktes ermittelt:
f(x) = -0,2x² + 0,6x + 2 = -0,2 [x² - 3x - 10] = -0,2 [x² - 3x + 1,5² - 2,25 - 10]= -0,2 [(x - 1,5)² - 12,25] = -0,2 (x - 1,5)² + 2,55
also S(1,5 / 2,55), was auch am Graph bestätigt werden kann.
Falls Sie auch nach längerem Überlegen mit den offenen Auftragsbeschreibungen nicht zurechtkommen, können Sie mit den Links am rechten Rand die konkreten Berechnungen anzeigen.
Aufgabe:
Führen Sie die oben beschriebenen Aufträge auch für nebenstehenden Graphen aus.
Hinweis: Nur die Punkte P1(-1/0), P2(4/0) und die Scheitelpunktkoordinate yS = -3 sind verlässlich bekannt.
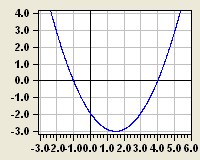
Lösung (aber zuerst selbst rechnen!)