Lösung:
zu 1a) und c) dick: G(f); dünn: G(f'); punktiert: G(f")
2a) und c) dick: G(f); dünn: G(f'); punktiert: G(f")
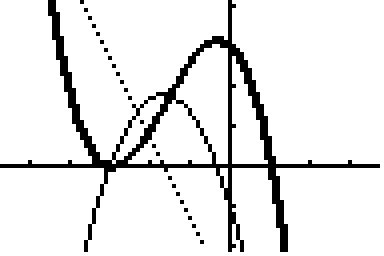
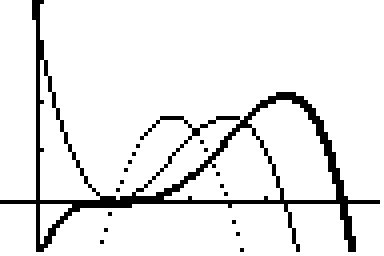
zu 1b) f(x) = a(x+3)²(x-1)
und mit f(0)=-9a=3 folgend a = -1/3
also f(x) = -1/3 x³
- 5/3 x² - x + 3
Dann ist f'(x) = -x² - 10/3 x - 1 und f"(x) = -2x - 10/3
zu 1b) f(x) = a(x-1)³(x-4)
und mit f(0) = 4a = -1 folgend a = -0,25
also f(x) = -0,25x^4
+ 1,75x³ - 3,75x² + 3,25x - 1
Dann ist f'(x) = -x³
+ 5,25x² - 7,5x + 3,25
und f"(x) = -3x² + 11x
- 7,5
zu 3a) und c) dick: G(f); dünn: G(f'); punktiert: G(f")
zu 4a) und c) dick: G(f); dünn: G(f'); punktiert: G(f")
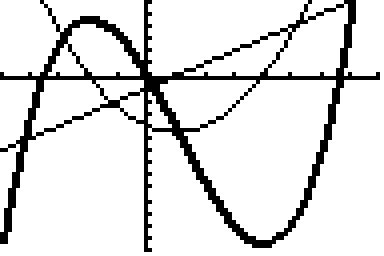
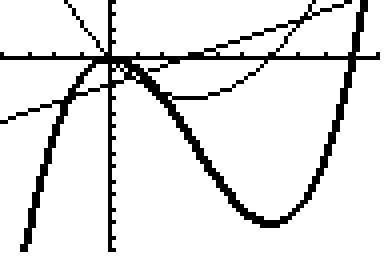
zu 3b) f'(x) = a(x+2)(x-4)
und mit f'(0) = -8a = -4 folgend a = 0,5
also f'(x) = 0,5x² - x - 4
Dann ist f(x) = 1/6 x³ - 0,5x² - 4x + d und f"(x)
= x - 1
zu 4b) f"(x) = 2/3 x - 2
Dann ist f'(x) = 1/3 x² - 2x + c (hier: c = 0)
und f(x) = 1/9 x³ - x² + cx + d (hier c=0 und d=0)
also f(x) = 1/9 x³ - x²