zu S.92; 3a) ms(x) = x² + 2x + 4
3b) ms(x) = x² + 0,5x + 0,25
3d) ms(x) = x² - x + 1
zu S.92; 4a) t(x) = 12x - 16
4b) t(x) = 3x + 2
4c) t(x) = 0
Unterrichtsbeispiel:
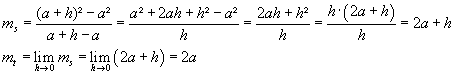
Polynomdivision:
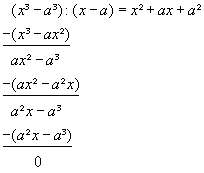
zu Lernportal Stufe 11 / Analysis / Interaktiv I3:
(Lösungen siehe dort)
zu S.92; 3) es wird jeweils verwendet: ms(x;a) = x² + ax + a²
zu S.92; 3b) ms(x;0,5) = x² + 0,5x + 0,25
zu S.92; 3c) ms(x;-2) = x² - 2x + 4
zu S.92; 3e) ms(x;0) = x² + 0x + 0² = x²
zu S.92; 3f) ms(x;-1,5) = x² - 1,5x + 2,25
zu S.92; 4) es wird jeweils verwendet: mt(a) = 3a²
zu S.92; 4a) mt(2) = 12 und t(x) = 12x - 16
zu S.92; 4b) mt(-1) = 3 und t(x) = 3x + 2
zu S.92; 4c) mt(0) = 0 und t(x) = 0x + 0 = 0
zu S.92; 4d) mt(-0,5) = 3(-0,5)² = 0,75 und t(x) = 0,75x + 0,25
[GTR]: Machen Sie
die Probe:
x³ als Y1 im Y-Editor, dann [Graph]
[II.Calc] 6 (dy/dx) (Eingabe x)
liefert die Tangentensteigung dort
[II. Draw] 5 (Tangent) (Eingabe x)
liefert Tangentengleichung und Graph
zu S.92; 6a)
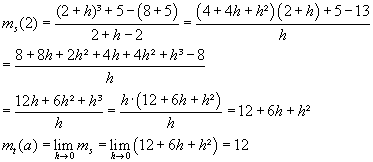
alternativ: Rechnung erst allgemein für a, damit dann
für a = 2
zu S.92; 6b) mt(0) =
0
zu S.92; 6c) mt(2) = 36
zu S.92; 6d) mt(1)
= 7
zu S.92; 6e) mt(2) = 14
zu S.92; 6f) mt(3)
= 12
Auch hier: Probe am GTR (s.o.)
Fazit: Die h->0 - Methode ist für Polynomfunktionen deutlich weniger geeignet!
zu S.92; 7a)
Es gibt
keine Stelle a, an der dieTangentensteigung 3a² = -4 ist.
zu
S.92; 7b) es soll also mt(a) = 0,75 gelten: (vgl. Buch
Seite 22)
Stellen a mit Steigung mt(a) = 0,75 :
mit mt(a) = 3a² (Buch S. 91) folgt 3a² = 0,75
, also a² = 0,25 ,
also sind a = -0,5 oder a = 0,5 die
gesuchten Berührstellen
Berührpunkte: P1(-0,5
/ -0,125) und P2(0,5 / 0,125)
Tangentengleichungen
- mittels Punkt/Steigungsform y-y1 = m(x-x1):
t1(x) + 0,125 = 0,75(x + 0,5) ,
also t1(x) = 0,75x + 0,375 - 0,125 = 0,75x + 0,25
t2(x) - 0,125 = 0,75(x - 0,5) ,
also t2(x) = 0,75x - 0,375 + 0,125 = 0,75x - 0,25
Auch hier: Probe am GTR (s.o.)
Zusätzlich:
- Ableitungsterm im Y-Editor als Y2 dazu mit [Math] 8 (nDerive):
nDerive(Y1,X,X) liefert immer den Tangentensteigungsterm zu Y1.
- Mit [Table] Wert 0,75 zu Y2 suchen, diese Stellen a in [II.Draw] 5 für X eingeben.
Zwischenübung:
Stellen a mit Tangenten an G(f) mit f(x) = x³ + 2x mit Steigung
mt(a) = 5
ms(x;a) = x² + ax + a² + 2 und mt(a) = 3a² + 2
Stellen a mit mt(a) = f'(a) = 5:
3a² + 2 = 5 , also 3a²
= 3 , also a² = 1 , also a = -1 oder a = +1
Berührpunkte:
P1(-1/-3) und P2(1/3)
Tangentengleichungen: t1(x) = 5x + 2 und
t2(x) = 5x - 2
Hier die ausführliche Lösung.
Auch hier: Probe am GTR (s.o.)
zu S. 95; 6d)
gegeben:
f(x) = (x-2)³ und P1(3/y) und P2(1/y)
Punktkoordinaten: P1(3/1) und P2(1/-1)
Leicht ist es, die konkrete Sekanten-/Tangentensteigung zu berechnen:
zu a=3: ms(x;3) = x² - 3x +3 und mt(3) = 9 - 9 + 3 = 3
zu a=1: ms(x;1) = x² - 5x + 7 und mt(1) = 1 - 5 + 7 = 3
Tangentengleichungen: t3(x) = 3x - 8 und t1(x) = 3x - 4
Sehr schwierig: allgemeine Steigungs-Berechnungen zur Stelle a:
allgemeine Sekantensteigung:
ms(x;a) = ( (x-2)³ - (a-2)³
) : (x - a) = x² + (a-6)x + a² - 6a + 12
allgemeine Tangentensteigung: mt(a) = f'(a) = 3a² - 12a + 12
Hier eine der konkreten Polynomdivisionen (zu ms(x;3)).
Hier die Polynomdivision zur Umformung von ms(x;a) (allgemein und schwierig).
[CAS]: Probe z.B. mit TI-89:
expand(((x-2)³-(t-2)³)/(x-t),x)
liefert hier z. B. den allg. Term
x²+x(t-6)+t²-6t+12 zu ms(x;t)
Wichtig: Variablen x und t dürfen keine Werte enthalten!
zu S. 95; 6a)
mt(2)
= 24 und t2(x) = 24x - 32
mt(-1) = 6 und t-1(x) = 6x + 4
oder Steigungen allgemein: ms(x;a) = 2x² + 2ax + 2a²
und mt(a) = 6a²
Auch hier: Probe am GTR (s.o.)
zu S. 95; 6c)
mt(-1)
= 4 und t-1(x) = 4x + 2
mt(2) = 13 und t2(x) = 13x - 16
oder Steigungen allgemein: ms(x;a) = x² + ax + a²
+ 1 und mt(a) = 3a²+1
Tipp: Versuchen Sie selbst die Polynomdivison zu ms(x;a) !
Auch hier: Probe am GTR (s.o.)
zu S. 95; 7a)
gegeben:
f(x) = x³ ; gesucht: Stellen a mit f'(a) = 27 [ bzw. 7 ; 0
]
mit f'(a) = 3a² (vgl. S. 91) folgt
3a² = 27,
also a² = 9, also a = -3 oder a = +3
3a² = 7, also
a² = 7/3 , also a = -Wurzel(7/3) oder a = +Wurzel(7/3)
3a² = 0, also a = 0
Auch hier: Probe am GTR (s.o.)
zu S. 95; 9a)
gegeben:
f(x) = x^4 ; gesucht: f'(1) [ bzw. f'(2) ; f'(0) ; f'(-4) ]
mit f'(a) = 4a³ (vgl. S. 94) folgt
f'(1) = 4 und f'(2)
= 32 und f'(0) = 0 und f'(-4) = -256
Auch hier: Probe am GTR (s.o.)