zu S. 63; 9
a) f(x) = (x+4)(x-2)(x+1)
= x³ + 3x² - 6x - 8
b) f(x) = (x+3)x(x-1)(x-2) = x^4
- 7x² + 6x
c) f(x) = x(x+3)(x-3)² = x^4 - 3x³
- 9x² + 27x
d) f(x) = -x³(x+4)² = -x^5 - 8x^4
-16x³
zu S. 64; 16
a) f(x) = x²(x+4)(x-3)
b) f(x) = (x+2)³(x-1)(x-3)
c) fx) = -0,001(x-5)(x-3)²(x+1)(x+4)²
Hinweis zu 16c):
mit a=-1 wäre
f(0) = -(-45).16 = 720
nun (mit a = -0,001):
f(0) = 0,72
zu S. 79; 28
a) f(x) = x(x+3)(x-1)
b) f(x) = x³(x+1)(x-2)
c) f(x) = -x²(x²-1)(x²-4)
Hinweis zu 28c):
a = -1, da Graph
von unten kommt
zu S. 96; 15:
a) y-Achse durch Scheitelpunkt;
dann f(x) = a(x-5)(x+5) und f(0) = -25a = 15,
also a = -0,6
; also f(x) = -0,6x² + 15
alternativ: f(x) = -0,6x²
+ 6x (mit Nullstellen x=0 u. x=10)
Hinweis zu 15a):
alternativ:
Nullstellen x=0 u. x=10
b) f'(x) = -1,2x und f'(-5) = 6 und
f(-5) = 0;
also t1(x) = 6(x + 5) + 0 = 6x + 30
f'(5) =
-6 und f(5) = 0 ; also f(x) = -6(x - 5) + 0 = -6x + 30
oder
alternativ (mit Nullstellen x=0 oder x=10) :
f'(x) = -1,2x
+ 6 und f'(0) = 6 ; also t1(x) = 6x
f'(10) = -12 + 6 = -6 ;
also t2(x) = -6x + 60
Hinweis zu 15b):
Punkt-Steigungsform
verwenden
c) tan(alpha) = 6/1 = 6 ; also alpha = 80,54°
tan(alpha) = Gegenk. / Ankathete
zu S. 103; 6
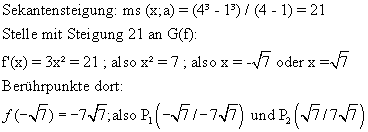
(Lösungen siehe dort)
zu S. 103; 11 (entspricht Ü4 Aufg.
2 im Lernportal Stufe 11 / Analysis)
a) f(x) = (x-1)(x+3)(x-27)
= x³ - 25x² - 5x + 81 und f'(x) = 3x² - 50x - 57
also f'(-1) = -4 und t(x) = -4x + 108 mit Nullstelle x = 27 (nach
t(x) = 0)
Die Tangente schneidet bei x=27 die x-Achse, dort
liegt auch die 3. Nullstelle.
b) (vgl. Lösung zu Ü4 Aufgabe 2)
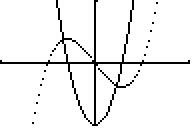
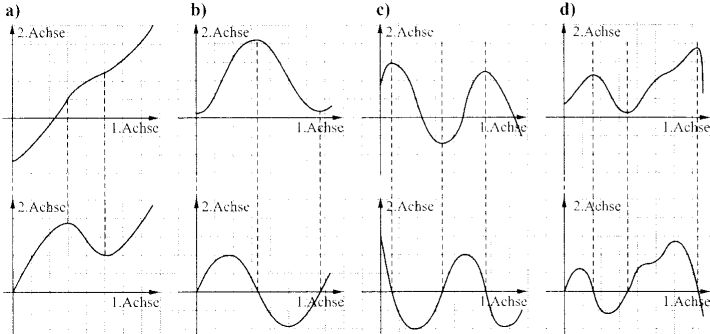
zu S. 116; 11 (dünn punktiert zusätzlich der Vorgabegraph G(f)! )
a) 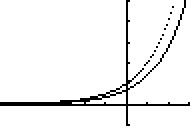 b)
b) 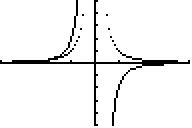
c)