Lösung:
für die Teilaufgabe (1) mit A(1/2), B(6/2) und C(3/4)
zu a) b = |AC| = 2,8 und a = |BC| =
3,6 und c = |AB| = 5 und A = 5 (gerundet!)
(mit zusätzlichem Schnittpunkt D(3/2) auf AB und Höhe
mit h = |CD| = 2)
zu b) b(x) = x + 1 und a(x) = -2/3 x + 6 und c(x) = 2
Hinweis: Ausführliche Lösungen siehe zu (3)
für die Teilaufgabe (2) mit A(-2/-1), B(5/5) und C(-2/5)
zu a) b = |AC| = 6 und a = |BC| = 7
und c = |AB| = 9,2 und A = 21 (gerundet!)
(wegen AC orthogonal zu BC sind dies geeignete Grundseite und Höhe!)
zu b) b: x = -2 (Parallele zur y-Achse!; falsch wäre: b(x)
= -2)
und a(x) = 5 (Parallele zur x-Achse!) und c(x) = 6/7 x
+ 5/7
Hinweis: Ausführliche Lösungen siehe zu (3)
für die Teilaufgabe (3) mit A(-2/-3), B(6/1) und C(1/4)
zu a)
Länge der Dreiecksseiten:
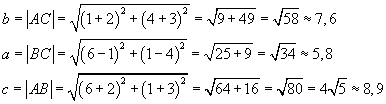
Dreiecksfläche:
Da kein rechter Innenwinkel (Weite 90°) existiert, muss eine
Höhe orthogonal zur Grundseite, deren Schnittpunkt mit der
Grundseite und deren Länge bestimmt werden. Als Grundseite
wird hier c=AB gewählt.
Steigung mh der Höhe: Wegen mc=1/2
muss mh=-2 gelten (s. Hinweis rechts).
Gleichung h(x) der Höhe: Weil C auf h liegt, gilt h:y-4=-2(x-1),
also h(x)=-2x+6
Schnittpunkt D zwischen h und c: h(x)=c(x), also -2x+6=0,5x-2 ,
also x=3,2
und h(3,2)=-6,4+6=-0,4 ; also D(3,2 / -0,4)
Länge der Höhe: ![]()
Fläche des Dreiecks: ![]()
Wenn g1 und g2
orthogonal zueinander sind, gilt für deren Steigungen: m1*m2=-1
.
Auch die Umkehrung gilt.
Punkt-Steigungsform:
Punkt (x1/y1), Steigung m
y-y1=m(x-x1)
zu b)
b=AC mit Methode 'erst m, dann n, dann b(x)',
also Einsetzen von m und z. B. C(1/4) in y=mx+n:
![]()
a=BC mit Zwei-Punkte-Form der Geradengleichung:![]()
c=AB durch Aufstellen und Lösen eines LGS,
also Einsetzen von A- und B-Koordinaten in allg. Form:
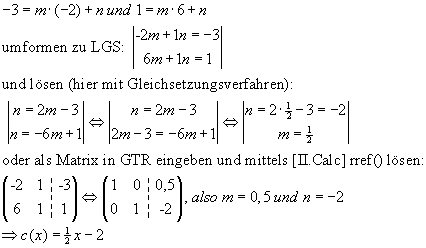
Allgemeine Form der Geradengleichung:
y = mx + n
Zwei-Punkte-Form:
(y-y1):(x-x1)=(y2-y1):(x2-x1)
Gerade durch LGS finden: