Aufgabe:
Einer nach unten geöffneten Parabel soll (im I. und II.
Quadranten) ein möglichst großes Dreieck einbeschrieben
werden, dessen Grundseite auf der x-Achse liegt, dessen Höhe
parallel zur y-Achse und bis zum Punkt P auf der Parabel verläuft.
Die Parabel ist von der Form der Normalparabel und hat die
Nullstellen x = -2,5 und x = 2,5.
a) Ermitteln Sie den Funktionsterm f(x) zur beschriebenen Parabel.
b) Berechnen Sie Grundseite, Höhe und Flächeninhalt
dieses größtmöglichen Dreiecks.
c) Welche Koordinaten
hat der Punkt P ?
d) Verschieben Sie die Parabel um 2 Einheiten
nach links. Bearbeiten Sie die Aufgabe erneut und zeigen Sie so,
dass die Maße des maximal großen Dreiecks unverändert
gelten.
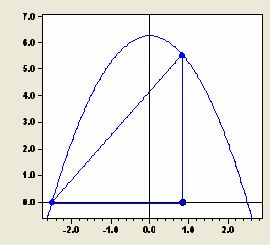
Der Graph wurde mit MatheAss
gezeichnet.