Aufgabe:
Aus einer Glasscheibe mit Flächeninhalt 2x5=10 FE, die wie abgebildet in zwei Scherben zerbrochen ist, soll ein möglichst großes, rechteckiges Reststück ausgeschnitten werden. Die Bruchkante sei durch einen Graph beschrieben, der von der Form der Normalparabel ist, als Hilfspunkt auf der Bruchkante dient P.
a) Ermitteln Sie den Funktionsterm f(x) zur beschriebenen Parabel.
b) Berechnen Sie Breite, Höhe und Flächeninhalt dieses
größtmöglichen Rechtecks. Untersuchen Sie auch mögliche
Randextrema.
c) Welche Koordinaten hat der Punkt P ?
d)
Untersuchen Sie, ob aus der zweiten (oberen) Scherbe ein - eventuell
sogar größeres - rechteckiges Reststück geschnitten
werden kann.
Skizze:
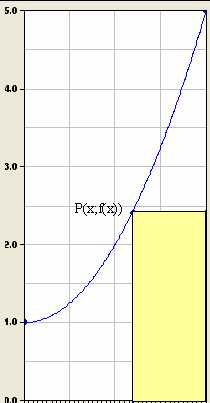
Der Graph wurde mit MatheAss
gezeichnet.