Übung 8
Themenbereich Anwendungsaufgaben (Betriebswirtschaft)
Lösungen:
zu c)
G(x) = E(x) - K(x) = 19x - x³ + 8x² - 25x - 12
also G(x) = -x³ + 8x² - 6x - 12
zu d)
bekannt: G(x) = -x³ + 8x² - 6x - 12
Erraten der ersten Nullstelle durch Probieren für x > 0 (wegen D(G)):
G(1) = -1 + 8 - 6 - 12 = - 11 <> 0
G(2) = -8 + 32 - 12 - 12 = 0
Ermitteln weiterer Nullstellen durch Polynomdivision und Nullsetzen des quadratischen
Ergebnisterms:
(-x³ + 8x² - 6x - 12) : (x - 2) = -x² + 6x + 6
-x² + 6x + 6 = 0 , also x² - 6x = 6 , also (x - 3)² = 6 + 9 =
15 ,
also x = 3 - Wu(15) - kein Element aus D(G) - oder x = 3 + Wu(15) = 6,9
Die Nullstellen in D(G) sind also x = 2 bzw. x = 6,9
Untersuchung auf Positivbereich durch bequeme Punktprobe zwischen den Nullstellen:
G(3) = -27 + 72 - 18 - 12 = 15 > 0 , also I3 = ] 2 ; 6,9 [
Die Gewinnzone liegt zwischen den Stückzahlen 2 ME und ca. 6,9 ME.
zu e)
Ableitungen:
G(x) = -x³ + 8x² - 6x - 12 und G '(x) = -3x² + 16x
- 6 und G "(x) = -6x + 16
Notwendige Bedingung:
G '(x) = 0 , also -3x² + 16x - 6 = 0 , also 3x² - 16x + 6 = 0 , also
3x² - 16x = -6 ,
also x² - 16/3 x = -2 , also (x - 8/3 x)² = -2 + 64/9 = -18/9 + 64/9
= 46/9 ,
also x = 8/3 - Wu(46/9) oder x = 8/3 + Wu(46/9),
also x = 2,67 - Wu(5,11) = 2,67 - 2,26 = 0,41 oder x = 2,67 + Wu(5,11) = 2,67
+ 2,26 = 4,93
Hinreichende Prüfung:
G "(0,41) = -2,46 + 16 = 13,54 > 0, hier liegt also ein relatives Minimum
G "(4,93) = -29,58 + 16 = -13,58 < 0, hier liegt also das gesuchte relative
Maximum
Zweite Koordinate an der Maximumstelle, also relatives Maximum:
G(4,93) = -119,82 + 194,44 - 29,58 - 12 = 33,04
Das Gewinnmaximum von 33,04 GE wird erzielt bei einer Stückzahl von ca.
4,93 ME.
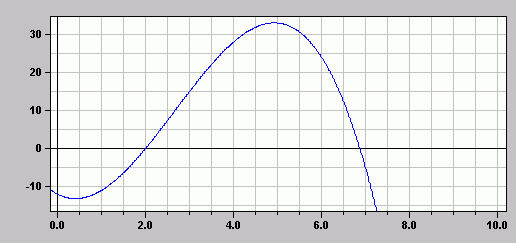
Zur Kontrolle: Graph der Gewinnfunktion G (erzeugt mit MatheAss)

© 2004 Ziemke .:. Letzte Aktualisierung am 10. Februar 2004 durch den WebMaster.