Übung 8
Themenbereich Anwendungsaufgaben (Betriebswirtschaft)
Lösungen:
zu f1)
Im folgenden bedeutet Ga: alte Gewinnfunktion und Gn: neue Gewinnfunktion
Vorüberlegungen:
Bisher galt: Ga(x) = -x³ + 8x² - 6x - 12
Durch den gesunkenen Absatzpreis gilt nun Gn(x) = -x³ + 8x² - 11x
- 12
Die Breite der Gewinnzone und der Maximalgewinn werden sich dadurch verringern.
Ermittlung der neuen Gewinnschwelle:
Die erste Nullstelle (Gewinnschwelle) muss nun weiter rechts liegen (Gewinn
erst bei größerer Stückzahl; bisher: x=2):
Gn(2) = -8 + 32 - 22 - 12 = -10 < 0
Gn(3) = -27 + 72 - 33 - 12 = 0
Die Gewinnschwelle liegt nun bei 3 ME.
Ermittlung der neuen Gewinngrenze und der Gewinnzone:
Die zweite Nullstelle (Gewinngrenze) muss (wegen der Verkleinerung der Gewinnzone)
nun weiter links liegen (bisher: x=6,9).
Für die Gewinngrenze ist nun wiederum eine Polynomdivision (Divisor x-3)
und das anschließende Lösen einer quadratischen Gleichung notwendig:
(-x³ + 8x² - 11x - 12) : (x-3) = -x² + 5x + 4
und aus -x² + 5x + 4 = 0 folgt x² - 5x = 4 , also (x-2,5)² =
4 + 6,25 = 10,25 ,
also x = 2,5 - Wu(10,25) < 0 (keine definierte Stückzahl) oder x = 2,5
+ Wu(10,25) = 2,5 + 0,5 * Wu(41) = 2,5 + 3,20 = 5,70
Die Gewinngrenze liegt bei ca. 5,70 ME.
Die neue Gewinnzone liegt nun zwischen den Stückzahlen von 3 und ca. 5,70
ME.
Ermittlung des Gewinnmaximums:
Ableitungen:
G(x) = -x³ + 8x² - 11x - 12 und G '(x) = -3x² + 16x
- 11 und G "(x) = -6x + 16
Notwendige Bedingung:
G '(x) = 0 , also -3x² + 16x - 11 = 0 , also 3x² - 16x + 11 = 0 ,
also 3x² - 16x = -11 ,
also x² - 16/3 x = -11/3 , also (x - 8/3 x)² = -11/3 + 64/9 = -33/9
+ 64/9 = 31/9 ,
also x = 8/3 - Wu(31/9) oder x = 8/3 + Wu(31/9),
also x = 2,67 - Wu(3,44) = 2,67 - 1,86 = 0,81 oder x = 2,67 + Wu(3,44) = 2,67
+ 1,86 = 4,53
Hinreichende Prüfung:
G "(0,81) = -4,86 + 16 = 11,14 > 0, hier liegt also ein relatives Minimum
G "(4,53) = -27,18 + 16 = -11,18 < 0, hier liegt also das gesuchte relative
Maximum
Zweite Koordinate an der Maximumstelle, also relatives Maximum:
G(4,53) = -92,96 + 164,17 - 49,83 - 12 = 9,38
Das Gewinnmaximum von 9,38 GE wird erzielt bei einer Stückzahl von ca.
4,53 ME.
Die Verringerung des erzielbaren Absatzpreises auf fast 75% des bisher erzielbaren
Preises
bewirkt also eine Maximalgewinnreduzierung auf weniger als 30% des bisherigen
Gewinnmaximums;
dieses Maximum wird bei annähernd der gleichen Stückzahl erreicht.
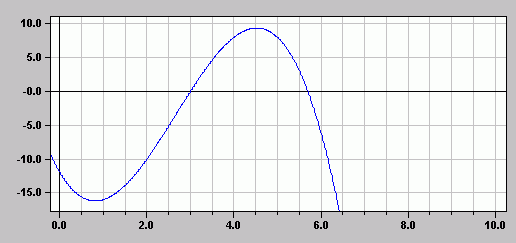
Zur Kontrolle: Graph der neuen Gewinnfunktion Gn (erzeugt mit MatheAss)

© 2004 Ziemke .:. Letzte Aktualisierung am 10. Februar 2004 durch den WebMaster.