Übung 8
Themenbereich Anwendungsaufgaben (Betriebswirtschaft)
Lösungen:
zu f2)
Im folgenden bedeutet Ga: alte Gewinnfunktion und Gn: neue Gewinnfunktion
Vorüberlegungen:
Bisher galt: Ga(x) = -x³ + 8x² - 6x - 12
Durch die gesenkten Fixkosten gilt nun Gn(x) = -x³ + 8x² - 6x - 7
Der Graph G(Gn) ergibt sich durch Verschiebung um 5 Einheiten nach oben aus
G(Ga).
Die Breite der Gewinnzone und das Gewinnmaximum werden sich dadurch vergrößern.
Ermittlung des Gewinnmaximums:
Das Gewinnmaximum wird um 5 GE vermehrt:
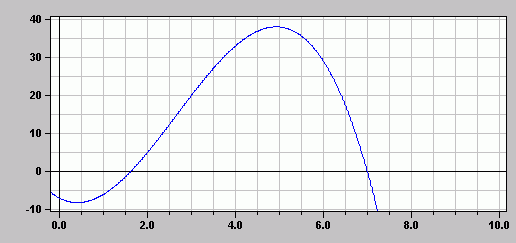
Das neue Gewinnmaximum von nun 38,04 GE wird ebenfalls bei einer Stückzahl
von ca. 4,93 ME erzielt.
Ermittlung von Gewinnschwelle und Gewinngrenze:
Die erste Nullstelle (Gewinnschwelle) muss (wegen der Verschiebung nach oben)
nun weiter links liegen (bisher: x=2):
Gn(1) = -1 + 8 - 6 - 7 = -6 < 0
Gn(2) = -8 + 32 - 12 - 7 = 5 > 0
Wie zu erwarten ist die erste Nullstelle nicht ganzzahlig, und es gilt 1 <
xn1 < 2.
Die zweite Nullstelle (Gewinngrenze) muss (wegen der Verschiebung nach oben)
nun weiter rechts liegen (bisher: x=6,9):
Gn(7) = -343 + 392 - 42 - 7 = 0
Die Gewinngrenze liegt nun bei genau 7 ME.
Für die Gewinngrenze ist nun wiederum eine Polynomdivision (Divisor x-7)
und das anschließende Lösen einer quadratischen Gleichung notwendig:
(-x³ + 8x² - 6x - 7) : (x-7) = -x² + x + 1
und aus -x² + x + 1 = 0 folgt x² - x = 1 , also (x-0,5)² = 1
+ 0,25 = 1,25 ,
also x = 0,5 - Wu(1,25) < 0 (keine definierte Stückzahl) oder x = 0,5
+ Wu(1,25) = 0,5 + 0,5 * Wu(5) = 1,62
Die neue Gewinnzone liegt nun zwischen den Stückzahlen ca. 1,62 ME und
7 ME.
Zur Kontrolle: Graph der neuen Gewinnfunktion Gn (erzeugt mit MatheAss)

© 2004 Ziemke .:. Letzte Aktualisierung am 10. Februar 2004 durch den WebMaster.