Übung 3
Aufgabe:
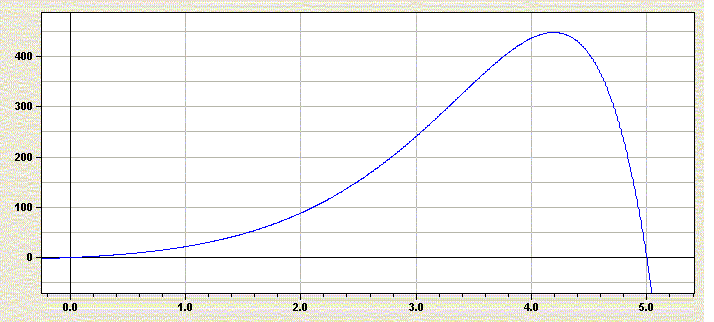
Gegeben sei der Graph der Funktion f mit f(x) = - 2x*(x-5)*e^x und
D(f)=[0 ; 5]:
f ordnet jeder Woche x (ab 1. März 2003: x=0) die Anzahl der in einem Blumenbeet
blühenden Osterglocken zu.
Hinweis: Die Stelle x=1,25 ergibt somit 1,25 * 7 = 8,75, meint also den
10. März 2003.

Zusätzlich seien gegeben:
Nullstellen: x=0 oder x=5
Tiefpunkt T (-1,19 / -4,48)
Hochpunkt H (4,19 / 448,15)
Wendepunkte W1 (-2,37 / -3,26) und W2 (3,37 / 319,96)
Beantworten Sie die folgenden Fragen ohne zusätzliche Rechnung, aber
mit Begründungen:
(Diese Begründungen müssen sich auf die verwendte(n) Eigenschaft(en)
des Graphen beziehen.)
(1) An wie vielen Tagen konnten blühende Osterglocken betrachtet werden?
(Achtung: 1 LE auf der x-Achse entspricht 1 Woche!)
(2) An welchem Tag blühten die meisten Osterglocken? Wie viele waren das?
(3) An welchem Tag kamen die meisten Blüten hinzu / verblühten die
meisten Osterglocken?
Zusätzliche Übungen:
(4) Berechnen Sie die Gleichung der Tangenten, die den Graph G(f) an der Stelle
x=4 [x=-2] berührt.
Hierbei sollten keine gerundeten Zahlen verwendet
werden, sondern genaue (z.B. 14e^x).
(5) Zusätzlich sei die Funktion g mit g(x)=e^x gegeben, deren Graph den
Graph G(f) zweimal schneidet.
Berechnen Sie das Maß der Fläche, die
vollständig im I. Quadranten liegt und durch beide Graphen
berandet wird. Berechnen Sie auch das Maß
der anderen (nicht vollständig berandeten) Fläche.
Lösungen
© 2004 Ziemke .:. Letzte Aktualisierung am 10. Februar 2004 durch den WebMaster.