zu 2 (1) a):
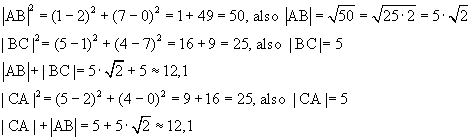
Beide Wege sind gleichlang,
nämlich ca. 12,1LE.
zu 2 (1) b):
Die Strecken AC und BC sind zueinander orthogonal:
Steigung der Strecke AC: mb = (5-2)/(4-0) = 3/4
Steigung
der Strecke BC: ma = (5-1)/(4-7)=-4/3
Produkt der
Steigungen: ma*mb = -1 (Orthogonalitätsbedingung
erfüllt)
Dies läßt sich auch leichter über
die Steigungsdreiecke zeigen.
Also können AC und BC Grundseite
und Höhe bilden:
Fläche des Dreiecks: F = 0,5 * |AC|
* |BC| = 0,5 * 5 * 5 = 12,5
Das Bau-Erwartungsland hat eine
Fläche von ca. 12,5 FE.
zu 2 (2) a): (Kurzlösung)
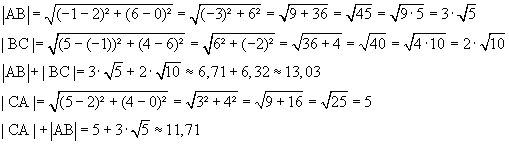
Der Weg von A über B nach C beträgt ca. 13,03LE, der von C über A nach B 11,71LE.
zu 2 (2) b): (Kurzlösung)
Da keine der Strecken zueinander
orthogonal sind, muss eine der Höhen bestimmt werden. Die Höhe
hc auf der Strecke AB hat die Länge 2LE, also hat
das Bau-Erwartungsland eine Fläche von ca. 6,71 FE.
(1) A(0/2), B(7/1), C(4/5)
(2) A(0/2),
B(6/-1), C(4/5)
Zurück zur Aufgabe oder weiter zur Lösung 3-5 (aber zuerst selbst rechnen!)