Kontroll-Lösungen:
- zu a)
-
Algebraisch: mit n0(x) = ax³ + bx² + cx + d
gilt z. B. n0(0,05) = 0,05³a + 0,05²b + 0,05c + 1d = 3,107
LGS mit vier Gleichungen aufstellen und lösen (sehr aufwändig)Mit GTR: Koeffizienten in Matrix-Editor eingeben:
z. B. erste Zeile: [0,05³ 0,05² 0,05 1 3,107],
mit rref() zugehörige Einheitsmatrix bilden
und daraus die Koeffizientenwerte zu a,b,c,d ablesen
Mit CAS: Define n0(x) = ax³ + bx² + cx + d
Kontroll-Lösung mit drei (gerundeten) Dezimalen:
und solve ( {4 Funktionalgleichungen},a,b,c,d) nutzen;
z. B. erste Funktionalgleichung: n0(0,05) = 3,107;
Eingabeschema für vier Gleichungen über ctrl-[x]-Taste!
n(x) = -105,518x³ + 15,614x² + 9,633x + 2,599 - zu b)
-
Achtung bei der Termeingabe: -106 2/3 x³ genau kontrollieren!
Beide Graphen sind trotz unterschiedlicher Koeffizienten im relevanten Bereich praktisch identisch. Anzeigebereich: z. B.
- zu c)
-
Nur nicht-negative Stellen x (für Düngermengen) und nur nicht-negative Funktionswerte (für Ernteerträge) sind für die Anwendung relevant. Also begrenzt die y-Achse und die Nullstelle x = 0,46 den Definitionsbereich für die Anwendung: D(h) = [0 ; 0,46]
- zu d)
-
(1) h(0,23) = -(106+2/3)*0,23³ + 16*0,23² + 9,6*0,23 + 2,6 = 4,357
(2) h'(x) = -320x² + 32x + 9,6 und h'(x) = 0 => x = 0,230
Die erste Lösung x = -0,130 liegt nicht in D(h)!
h"(x) = -640x + 32 und h"(0,230) = -115,4 < 0 => rel. Maximum bei x=0,23(3)
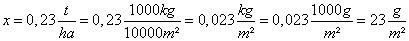
(4) maxmehr = h(0,23) - h(0) = 4,357 - 2,6 = 1,757
(5) mit maxmehr = 1,757 folgt
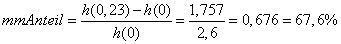 ;
die Angabe 'mehr als 50%' ist also korrekt - eine deutliche Ertragssteigerung durch Düngung!
;
die Angabe 'mehr als 50%' ist also korrekt - eine deutliche Ertragssteigerung durch Düngung!
- zu e)
-
h"(x) = -640x + 32 und h"(x) = 0 => x = 0,05
h"'(x) = -640 und h"'(0,05) = -640 < 0 => L/R-Wendepunkt bei x=0,05
h'(0,05) = -320*0,05² + 32*0,05 + 9,6 = 10,4Für die Zugabe von 0,05 t/ha Dünger wird der Ernteertrag am stärksten zunehmen, hier liegt für die Funktion die maximale Steigung (m=10,4) vor. Die Änderungsrate beträgt 10,4 t Raps pro eingesetzte Tonne Dünger bei Zugabe von 0,05 t/ha. Dies sollte nicht mit dem größten Ernteertrag (4,357 t/ha) bei Zugabe von 0,23 t/ha Dünger verwechselt werden.



- zu f)
-
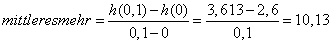 Die durchschnittliche Ertragszuwachsrate für Düngerzugaben bis 0,1 t/ha
mit 10,14 (Tonnen Raps pro Tonne Dünger) entspricht am Graph von h
der Steigung der Sekante durch die Graphenpunkte (0 ; 2,6) und (0,1 ; 3,613).
Die durchschnittliche Ertragszuwachsrate für Düngerzugaben bis 0,1 t/ha
mit 10,14 (Tonnen Raps pro Tonne Dünger) entspricht am Graph von h
der Steigung der Sekante durch die Graphenpunkte (0 ; 2,6) und (0,1 ; 3,613).
- zu g)
-
(1) Im Term g(x) muss der Ertrag für die Erntemenge um den Kostenaufwand für die Düngung reduziert werden, also Erntemenge*Ertrag - Düngermenge*Kosten: g(x) = 225*h(x) - 500*x. (mit CAS: Define g(x) = 225*h(x) - 500*x)
(2)
(3) Der Wert g(0,23) für den Gewinn bei optimaler Düngung muss mit der Feldgröße 13,2 multipliziert werden: Dies ergibt einen maximalen Gewinn von ca. 11421 Euro für den Bauern. Eine solche Feldgröße ist in Deutschland eher unterdurchschnittlich. Da Raps nur einmal pro Jahr angebaut werden kann und das Feld zwischenzeitlich nicht gewinnbringend nutzbar ist, muss der Landwirt noch weitere Einnahmen (Felderträge, Viehzucht,...) haben, um eine auskömmliche Jahreseinnahme zu erhalten. Die Polynomdarstellung von g(x) entspricht der des angegebenen Hilfsterms:
Die Polynomdarstellung von g(x) entspricht der des angegebenen Hilfsterms:
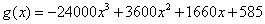 (mit CAS: expand(g(x)) )
(mit CAS: expand(g(x)) )
(4) Mit CAS: fMax (g(x),x,0,0.6) liefert x = 0,209861 , also x = 0,210
g(0,21) liefert 11485,3 , also einen etwas höheren Gewinn. Die Kosten für den Dünger drücken also ab einer Düngerbeigabe von 0,21 t/ha den Gewinn, obwohl der Ernteertrag noch gesteigert wird, der Raps-Abgabepreis am Markt aber einen optimaleren Gewinn verhindert.