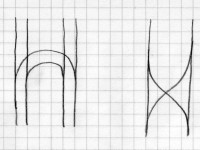 Vorüberlegungen:
Vorüberlegungen:
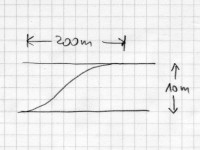
Hier sind anfangs unterschiedliche Darstellungen der vom Text erhaltenen
Informationen zu erwarten. Insbesondere auf die Formulierung '...
auf eine Länge von 200m ...' und Informationen daraus ist zu
achten. Zur Zweckerfüllung ist kein VerbindungsKREUZ notwendig.
 Erster Mathematisierungsschritt:
Erster Mathematisierungsschritt:
Der Prozess der Mathematisierung erfordert eine Festlegung, in welcher
Weise möglichst geschickt das Koordinatensystem eingefügt
wird. Dadurch entfallen bereits Ansätze, in denen die vorhandenen
Gleise als Parallelen zur y-Achse skizziert sind, da zu diesen Geraden
keine im Weiteren notwendigen Steigungen existieren. Gleichartige
Maßeinheiten (m oder km) auf beiden Achsen sind nötig.
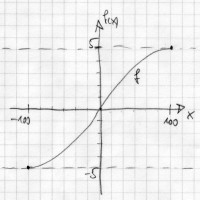 Variante 1
Variante 1
Tragfähig für die weitere
Bearbeitung verbleiben dann zwei Varianten:
die rechts oben
dargestellte und die nebenstehende. Hier soll die nebenstehende
Variante 2 verfolgt werden.
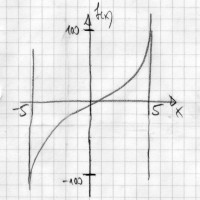
Im weiteren Mathematisierungsschritt sollte die Problemstellung
als eine zu lösende Steckbriefaufgabe erkannt werden. Die gesuchte
Funktion muss (mindestens) vom dritten Grad sein (wegen des Wendepunktes).
Die Koordinaten der Anschlusspunkte und die Steigungen dort ergeben
vier Funktionalgleichungen:
f(0) = 0 und f(200) = 10 und f'(0)
= 0 und f'(200) = 0 sowie später zu prüfen: f"(0)
> 0 und f"(200) = < 0 .
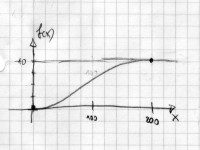 Variante 2
Variante 2
Daraus resultieren als Parametergleichungen:
d = 0 und 8000000a + 40000b + 200c = 10 und
c = 0 und 120000a + 400b = 0 (da c=0
bereits bekannt).
f(x) = ax³ + bx² + cx + d
f'(x) = 3ax² + 2bx + c
f"(x) = 6ax + 2b
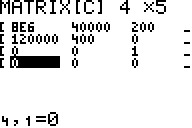 Dieses LGS lassen wir mit dem
CAS oder dem GTR lösen:
Dieses LGS lassen wir mit dem
CAS oder dem GTR lösen:
Wir geben im MatrixEditor die Koeffizienten
ein und wandeln diese erweiterte Matrix mittels rref()-Befehl um
in eine erweiterte Einheitsmatrix. Als Parameterwerte erhalten wir:
a = -2,5*10-6 und b = 7,5*10-4
; also f(x) = -0,0000025x³ + 0,00075x²
Die Überprüfung der hinreichenden Bedingungen ergibt,
dass diese erfüllt sind; als Funktion 3. Grades ist dies die
einzige Lösung.
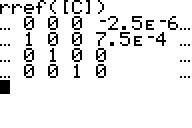
rref() aufrufen mittels (TI-84):
[II.Matrix] MATH [III.B]
([II.Matrix] meint [2nd][Matrix])
Würde als Maßeinheit statt m die Einheit km verwendet, hätten die Koeffizienten 'angenehmere' Größen: a = -2500 und b = 750.
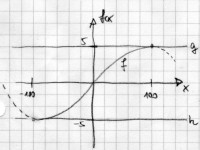
Die Variante 1 mit Wendepunkt im Ursprung
wäre für die Bearbeitung etwas bequemer gewesen - selbst
wenn man keine Wendepunktbedingung verwendet, da diese nicht unmittelbar
dem Text zu entnehmen ist. Die Funktionalgleichungen sind dann f(-100)
= -5 und f(100) = 5 und f'(-100) = 0 und f'(100) = 0.
Die Lösungsfunktion
hätte (wegen der Punktsymmetrie zum Ursprung) dann die Gleichung
f(x) = -2,5*10-6x³ + 0,075x (bei Verwendung der
Maßeinheit m).
In einer weiterführenden Diskussion
sollte erkannt werden, dass die Annahme, an den Anschlussstellen
liegen Extrempunkte, die Anzahl der möglichen Lösungen
einschränkt. Da der Verlauf vor und nach dem für die Anwendung
wichtigen Definitionsbereich D(f) = [ -100 ; 100 ] unterschiedlich
sein kann, sind in den Anschlusspunkten Extrempunkte oder auch Sattelpunkte
denkbar. Dadurch ergeben sich dann auch Lösungsfunktionen vierten
und sogar fünften Grades!
f"(-100) = 0 und/oder f"(100)
= 0 sind/ist die zusätzliche(n) Funktionalgleichung(en).