(1) gegeben: n = 1200 ; p0 = 0,1 ; alpha = 0,05 ; p1 = 0,12
Berechnungen:
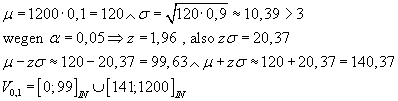

Testhypothese Ho:
Eine beliebige der zehn möglichen Superzahlen wird beobachtet.
Man testet, ob diese Zahl gleichwahrscheinlich mit den übrigen
eintritt, also durchschnittlich in 10% der Ziehungen.
Entscheidungsregel:
Verwerfe die Hypothese, dass die Superzahlen
gleichverteilt auftreten, falls in der Serie von 1200 höchstens
99 oder mindestens 141 mal eine der zehn möglichen Zahlen eintritt.
(2) Mögliche Fehler
beim Testen:
Die Stichprobe zeigt ein unwahrscheinliches (weil
zu seltenes oder zu häufiges) Auftreten der beobachteten Superzahl,
obwohl sie im allgemeinen gleich häufig wie die übrigen
eintritt. Daher wird die Hypothese - alle Zahlen werden etwa gleich
häufig gezogen - abgelehnt; Fehler 1. Art.
Wegen eines
mit der Gleichverteilung verträglichen Testergebnisses (zwischen
100 und 140 Eintreten der beobachteten Superzahl) wird die Hypothese
nicht abgelehnt; tatsächlich aber erscheint diese Superzahl
(z. B. in weiteren Ziehungen) seltener oder häufiger; Fehler
2. Art).
(3) Fehlerwahrscheinlichkeit
ß zu p1=0.12:
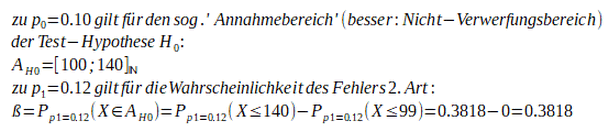
(korrigiert nach Hinweis von Martin P. - Danke!)
Skizze:
[*****************]
--100---------------140--
VH0 AH0 VH0
Antwort:
Der Fehler 2. Art - ein zu unregelmäßiges
Auftreten der Superzahl 0 (nämlich zu 12%) wird nicht erkannt
- geschieht ca. 38,2% wahrscheinlich.
Zurück zur Aufgabe