Lösung der Teilaufgaben a-d):
zu a)
bekannt: n = 10 und X: Anzahl
der gleichzeitig benötigten Telefonleitungen
mit p = 12/60
= 1/5 = 0,2 und k = 3
(Die drei Leitungen reichen aus, wenn
höchstens so viele Leitungen gleichzeitig benötigt werden,
wie Telefonleitungen zur Verfügung stehen:)
![]()
Die drei Leitungen reichen
in 87,9% der Dienstzeit aus.
zu b)
bekannt: n, X, p (siehe a), k = 4
![]()
Nein, auch vier Leitungen
würden nicht genügen, da in 3,3% der Fälle keine
freie Leitung verfügbar wäre.

zu c)
bekannt: n = 20
und X: Anzahl der gleichzeitig benötigten Telefonleitungen
mit p = 10/60 = 1/6 und k = 3
(Ein Mitarbeiter erhält keine
freie Leitung, wenn bereits mindestens drei Leitungen besetzt sind:)
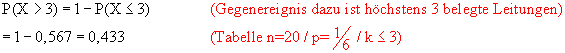
Obwohl die nun zwanzig Mitarbeiter weniger häufig telefonieren,
werden sie in 43,3% der Fälle keine freie Leitung erhalten.
zu d)
bekannt: (n, X,
p siehe c)
gesucht: k mit

Man wird fünf Amtsleitungen einrichten,
um annährend eine Verfügbarkeit von mindestens 90% für
eine freie Leitung sicherzustellen. Die Einrichtung einer sechsten
Leitung erscheint unnötig (fast 90%).